Rational curve
A one-dimensional algebraic variety, defined over an algebraically closed field 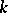 , whose field of rational functions is a purely transcendental extension of degree 1 of
, whose field of rational functions is a purely transcendental extension of degree 1 of  . Every non-singular complete rational curve is isomorphic to the projective line
. Every non-singular complete rational curve is isomorphic to the projective line  . A complete singular curve
. A complete singular curve 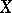 is rational if and only if its geometric genus
is rational if and only if its geometric genus 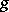 is zero, that is, when there are no regular differential forms on
is zero, that is, when there are no regular differential forms on 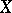 .
.
When 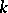 is the field
is the field 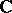 of complex numbers, the (only) non-singular complete rational curve
of complex numbers, the (only) non-singular complete rational curve 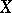 is the Riemann sphere
is the Riemann sphere 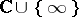 .
.
Comments
In classic literature a rational curve is also called a unicursal curve.
If 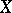 is defined over a not necessarily algebraically closed field
is defined over a not necessarily algebraically closed field  and
and  is birationally equivalent to
is birationally equivalent to 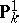 over
over  ,
, 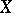 is said to be a
is said to be a 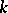 -rational curve.
-rational curve.
References
| [a1] | W. Fulton, "Algebraic curves" , Benjamin (1969) pp. 66 MR0313252 MR0260752 Zbl 0194.21901 Zbl 0181.23901 |
| [a2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Rational curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_curve&oldid=23948