Rao-Cramér inequality
Cramér–Rao inequality, Fréchet inequality, information inequality
An inequality in mathematical statistics that establishes a lower bound for the risk corresponding to a quadratic loss function in the problem of estimating an unknown parameter.
Suppose that the probability distribution of a random vector 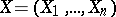 with values in the
with values in the  -dimensional Euclidean space
-dimensional Euclidean space 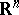 is defined by a density
is defined by a density 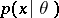 ,
, 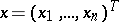 ,
, 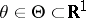 . Suppose that a statistic
. Suppose that a statistic 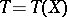 such that
such that
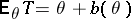 |
is used as an estimator for the unknown scalar parameter 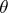 , where
, where 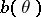 is a differentiable function, called the bias of
is a differentiable function, called the bias of 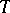 . Then under certain regularity conditions on the family
. Then under certain regularity conditions on the family 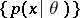 , one of which is that the Fisher information
, one of which is that the Fisher information
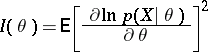 |
is not zero, the Cramér–Rao inequality
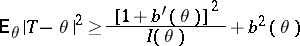 | (1) |
holds. This inequality gives a lower bound for the mean-square error 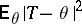 of all estimators
of all estimators 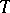 for the unknown parameter
for the unknown parameter 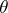 that have the same bias function
that have the same bias function 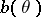 .
.
In particular, if 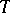 is an unbiased estimator for
is an unbiased estimator for 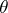 , that is, if
, that is, if 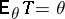 , then (1) implies that
, then (1) implies that
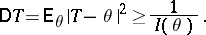 | (2) |
Thus, in this case the Cramér–Rao inequality provides a lower bound for the variance of the unbiased estimators 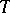 for
for 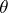 , equal to
, equal to 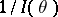 , and also demonstrates that the existence of consistent estimators (cf. Consistent estimator) is connected with unrestricted growth of the Fisher information
, and also demonstrates that the existence of consistent estimators (cf. Consistent estimator) is connected with unrestricted growth of the Fisher information 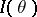 as
as 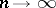 . If equality is attained in (2) for a certain unbiased estimator
. If equality is attained in (2) for a certain unbiased estimator 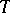 , then
, then 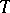 is optimal in the class of all unbiased estimators with regard to minimum quadratic risk; it is called an efficient estimator. For example, if
is optimal in the class of all unbiased estimators with regard to minimum quadratic risk; it is called an efficient estimator. For example, if 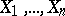 are independent random variables subject to the same normal law
are independent random variables subject to the same normal law 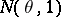 , then
, then 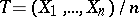 is an efficient estimator of the unknown mean
is an efficient estimator of the unknown mean 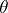 .
.
In general, equality in (2) is attained if and only if 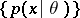 is an exponential family, that is, if the probability density of
is an exponential family, that is, if the probability density of 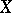 can be represented in the form
can be represented in the form
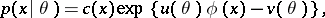 |
in which case the sufficient statistic 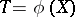 is an efficient estimator of its expectation
is an efficient estimator of its expectation 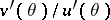 . If no efficient estimator exists, the lower bound of the variances of the unbiased estimators can be refined, since the Cramér–Rao inequality does not necessarily give the greatest lower bound. For example, if
. If no efficient estimator exists, the lower bound of the variances of the unbiased estimators can be refined, since the Cramér–Rao inequality does not necessarily give the greatest lower bound. For example, if 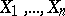 are independent random variables with the same normal distribution
are independent random variables with the same normal distribution 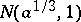 , then the greatest lower bound to the variance of unbiased estimators of
, then the greatest lower bound to the variance of unbiased estimators of  is equal to
is equal to
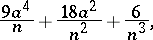 |
while
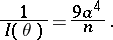 |
In general, absence of equality in (2) does not mean that the estimator that has been found is not optimal, since it may well be the only unbiased estimator.
There are different generalizations of the Cramér–Rao inequality, to the case of a vector parameter, or to that of estimating a function of the parameter. Refinements of the lower bound in (2) play an important role in such cases.
The inequality (1) was independently obtained by M. Fréchet, C.R. Rao and H. Cramér.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | L.N. Bol'shev, "A refinement of the Cramér–Rao inequality" Theory Probab. Appl. , 6 (1961) pp. 295–301 Teor. Veryatnost. Primenen. , 6 : 3 (1961) pp. 319–326 |
| [4a] | A. Bhattacharyya, "On some analogues of the amount of information and their uses in statistical estimation, Chapt. I" Sankhyā , 8 : 1 (1946) pp. 1–14 |
| [4b] | A. Bhattacharyya, "On some analogues of the amount of information and their uses in statistical estimation, Chapt. II-III" Sankhyā , 8 : 3 (1947) pp. 201–218 |
| [4c] | A. Bhattacharyya, "On some analogues of the amount of information and their uses in statistical estimation, Chapt. IV" Sankhyā , 8 : 4 (1948) pp. 315–328 |
Comments
References
| [a1] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
Rao-Cramér inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rao-Cram%C3%A9r_inequality&oldid=13110