Rank vector
A vector statistic (cf. Statistics) 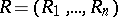 constructed from a random observation vector
constructed from a random observation vector 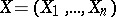 with
with 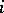 -th component
-th component 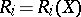 ,
, 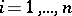 , defined by
, defined by
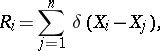 |
where 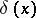 is the characteristic function (indicator function) of
is the characteristic function (indicator function) of 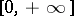 , that is,
, that is,
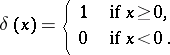 |
The statistic  is called the rank of the
is called the rank of the 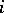 -th component
-th component 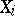 ,
, 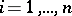 , of the random vector
, of the random vector 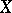 . This definition of a rank vector is precise under the condition
. This definition of a rank vector is precise under the condition
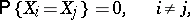 |
which automatically holds if the probability distribution of 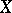 is defined by a density
is defined by a density  . It follows from the definition of a rank vector that, under these conditions,
. It follows from the definition of a rank vector that, under these conditions, 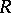 takes values in the space
takes values in the space 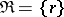 of all permutations
of all permutations  of
of 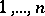 and the realization
and the realization 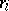 of the rank
of the rank  is equal to the number of components of
is equal to the number of components of 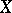 whose observed values do not exceed the realization of the
whose observed values do not exceed the realization of the 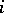 -th component
-th component 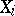 ,
, 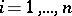 .
.
Let 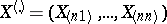 be the vector of order statistics (cf. Order statistic) constructed from the observation vector
be the vector of order statistics (cf. Order statistic) constructed from the observation vector 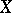 . Then the pair
. Then the pair 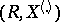 is a sufficient statistic for the distribution of
is a sufficient statistic for the distribution of 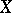 , and
, and 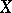 itself can be uniquely recovered from
itself can be uniquely recovered from 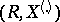 . Moreover, under the additional assumption that the density
. Moreover, under the additional assumption that the density 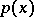 of
of 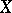 is symmetric with respect to permutations of the arguments, the components
is symmetric with respect to permutations of the arguments, the components 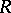 and
and 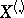 of the sufficient statistic
of the sufficient statistic 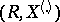 are independent and
are independent and
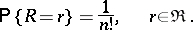 |
In particular, if
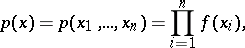 | (1) |
that is, the components 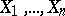 are independent identically-distributed random variables (
are independent identically-distributed random variables (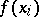 stands for the density of
stands for the density of 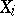 ), then
), then
 | (2) |
for any  .
.
If (1) holds, there is a joint density 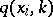 ,
, 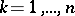 , of
, of 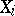 and
and 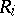 , defined by the formula
, defined by the formula
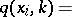 | (3) |
 |
where 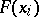 is the distribution function of
is the distribution function of 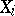 . It follows from (2) and (3) that the conditional density
. It follows from (2) and (3) that the conditional density 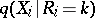 of
of  given
given 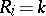 (
(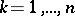 ) is expressed by the formula
) is expressed by the formula
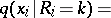 | (4) |
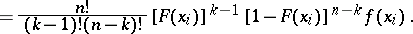 |
The latter formula allows one to trace the internal connection between the observation vector 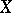 , the rank vector
, the rank vector  and the vector
and the vector 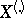 of order statistics, since (4) is just the probability density of the
of order statistics, since (4) is just the probability density of the 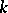 -th order statistic
-th order statistic 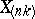 ,
, 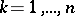 . Moreover, it follows from (3) that the conditional distribution of the rank
. Moreover, it follows from (3) that the conditional distribution of the rank 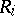 is given by the formula
is given by the formula
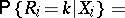 |
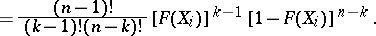 |
Finally, under the assumption that the moments 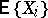 and
and 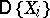 exist and that (1) holds, (2) and (3) imply that the correlation coefficient
exist and that (1) holds, (2) and (3) imply that the correlation coefficient 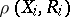 between
between 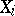 and
and 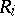 is equal to
is equal to
 |
In particular, if 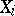 is uniformly distributed on
is uniformly distributed on 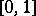 , then
, then
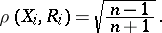 |
If 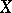 has the normal distribution
has the normal distribution 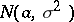 , then
, then
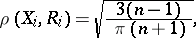 |
and 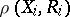 does not depend on the parameters of the normal distribution.
does not depend on the parameters of the normal distribution.
References
| [1] | W. Hoeffding, " "Optimum" nonparametric tests" , Proc. 2nd Berkeley Symp. Math. Stat. Probab. (1950) , Univ. California Press (1951) pp. 83–92 |
| [2] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [3] | F.P. Tarasenko, "Non-parametric statistics" , Tomsk (1976) (In Russian) |
Rank vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_vector&oldid=15810