Rank statistic
A statistic (cf. Statistical estimator) constructed from a rank vector. If  is the rank vector constructed from a random observation vector
is the rank vector constructed from a random observation vector  , then any statistic
, then any statistic  which is a function of
which is a function of 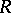 is called a rank statistic. A classical example of a rank statistic is the Kendall coefficient of rank correlation
is called a rank statistic. A classical example of a rank statistic is the Kendall coefficient of rank correlation  between the vectors
between the vectors 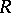 and
and  , defined by the formula
, defined by the formula
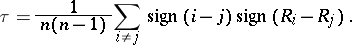 |
In the class of all rank statistics a special place is occupied by so-called linear rank statistics, defined as follows. Let  be an arbitrary square matrix of order
be an arbitrary square matrix of order  . Then the statistic
. Then the statistic
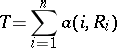 |
is called a linear rank statistic. For example, the Spearman coefficient of rank correlation 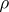 , defined by the formula
, defined by the formula
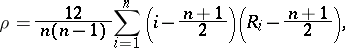 |
is a linear rank statistic.
Linear rank statistics are, as a rule, simple to construct from the computational point of view and their distributions are easy to find. For this reason the notion of projection of a rank statistic into the family of linear rank statistics plays an important role in the theory of rank statistics. If 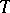 is a rank statistic constructed from a random vector
is a rank statistic constructed from a random vector 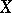 under a hypothesis
under a hypothesis 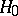 about its distribution, then a linear rank statistic
about its distribution, then a linear rank statistic 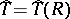 such that
such that 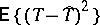 is minimal under the condition that
is minimal under the condition that 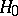 is true, is called the projection of
is true, is called the projection of 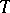 into the family of linear rank statistics. As a rule,
into the family of linear rank statistics. As a rule,  approximates
approximates 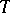 well enough and the difference
well enough and the difference 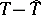 is negligibly small as
is negligibly small as 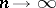 . If the hypothesis
. If the hypothesis 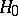 under which the components
under which the components 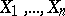 of the random vector
of the random vector  are independent random variables is true, then the projection
are independent random variables is true, then the projection 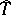 of
of 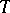 can be determined by the formula
can be determined by the formula
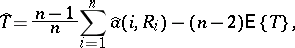 | (*) |
where  ,
, 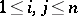 (see [1]).
(see [1]).
There is an intrinsic connection between  and
and 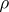 . It is shown in [1] that the projection
. It is shown in [1] that the projection 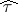 of the Kendall coefficient
of the Kendall coefficient  into the family of linear rank statistics coincides, up to a multiplicative constant, with the Spearman coefficient
into the family of linear rank statistics coincides, up to a multiplicative constant, with the Spearman coefficient  ; namely,
; namely,
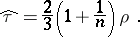 |
This equality implies that the correlation coefficient 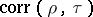 between
between  and
and  is equal to
is equal to
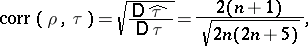 |
implying that these rank statistics are asymptotically equivalent for large  (cf. [2]).
(cf. [2]).
References
| [1] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [2] | M.G. Kendall, "Rank correlation methods" , Griffin (1970) |
Rank statistic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_statistic&oldid=18903