Rank of a group
(general and special rank of a group)
A notion from group theory. A group 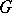 has finite general rank
has finite general rank  if
if  is the minimal number such that any finitely-generated subgroup of
is the minimal number such that any finitely-generated subgroup of  is contained in a subgroup having
is contained in a subgroup having  generators
generators 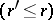 . A group
. A group  has finite special rank
has finite special rank  if
if  is the minimal number such that any finitely-generated subgroup of
is the minimal number such that any finitely-generated subgroup of 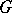 has a system of generators of at most
has a system of generators of at most  elements. If no such finite number exists, then the general (special) rank of the group is said to be infinite.
elements. If no such finite number exists, then the general (special) rank of the group is said to be infinite.
The general rank of a group is smaller than or equal to its special rank. There are groups with finite general rank (even equal to two) and infinite special rank. Such is, for instance, the countable symmetric group. For an Abelian group the general and special rank coincide with its Prüfer rank (see Abelian group).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
Rank of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_a_group&oldid=14796