Difference between revisions of "Random variables, transformations of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (dead link removed) |
||
| Line 21: | Line 21: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737021.png" /></td> </tr></table> | ||
| − | Example 3. The random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737024.png" /> are asymptotically normal as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737025.png" /> (see [[ | + | Example 3. The random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737024.png" /> are asymptotically normal as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737025.png" /> (see [[Chi-squared distribution| Chi-squared distribution]]). The uniform deviation of the corresponding distribution functions from their normal approximations becomes less than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737026.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737027.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737028.png" />, and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737029.png" /> (the Fisher transformation) — when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737030.png" />; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737031.png" /> (the Wilson–Hilferty transformation) when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737032.png" /> this deviation does not exceed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077370/r07737033.png" />. |
Transformations of random variables have long been applied in problems of mathematical statistics as the basis for constructing simple asymptotic formulas of high precision. Transformations of random variables are also used in the theory of stochastic processes (for example, the method of the "single probability space" ). | Transformations of random variables have long been applied in problems of mathematical statistics as the basis for constructing simple asymptotic formulas of high precision. Transformations of random variables are also used in the theory of stochastic processes (for example, the method of the "single probability space" ). | ||
Revision as of 12:03, 20 October 2012
The determination of functions of given arbitrary random variables for which the probability distributions possess given properties.
Example 1. Let  be a random variable having a continuous and strictly increasing distribution function
be a random variable having a continuous and strictly increasing distribution function  . Then the random variable
. Then the random variable  has a uniform distribution on the interval
has a uniform distribution on the interval  , and the random variable
, and the random variable  (where
(where  is the standard normal distribution function) has a normal distribution with parameters 0 and 1. Conversely, the formula
is the standard normal distribution function) has a normal distribution with parameters 0 and 1. Conversely, the formula  enables one to obtain a random variable
enables one to obtain a random variable  that has the given distribution function
that has the given distribution function  from a random variable
from a random variable 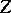 with a standard normal distribution.
with a standard normal distribution.
Transformations of random variables are often used in connection with limit theorems of probability theory. For example, let a sequence of random variables 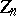 be asymptotically normal with parameters
be asymptotically normal with parameters  . One then poses the problem of constructing simple (and simply invertible) functions
. One then poses the problem of constructing simple (and simply invertible) functions 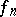 such that the random variables
such that the random variables  are "more normal" than
are "more normal" than 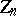 .
.
Example 2. Let 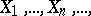 be independent random variables, each having a uniform distribution on
be independent random variables, each having a uniform distribution on 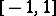 , and put
, and put
 |
By the central limit theorem,
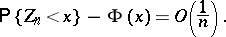 |
If one sets
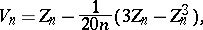 |
then
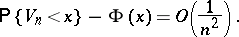 |
Example 3. The random variables 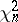 ,
, 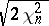 and
and  are asymptotically normal as
are asymptotically normal as  (see Chi-squared distribution). The uniform deviation of the corresponding distribution functions from their normal approximations becomes less than
(see Chi-squared distribution). The uniform deviation of the corresponding distribution functions from their normal approximations becomes less than  for
for  when
when 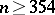 , and for
, and for 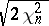 (the Fisher transformation) — when
(the Fisher transformation) — when 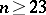 ; for
; for  (the Wilson–Hilferty transformation) when
(the Wilson–Hilferty transformation) when 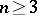 this deviation does not exceed
this deviation does not exceed 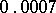 .
.
Transformations of random variables have long been applied in problems of mathematical statistics as the basis for constructing simple asymptotic formulas of high precision. Transformations of random variables are also used in the theory of stochastic processes (for example, the method of the "single probability space" ).
References
| [1] | L.N. Bol'shev, "On transformations of random variables" Theory Probab. Appl. , 4 (1959) pp. 129–141 Teor. Veryatnost. Primenen. , 4 : 2 (1959) pp. 136–149 |
| [2] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theory Probab. Appl. , 8 : 2 (1963) pp. 121–146 Teor. Veroyatnost. Primenen. , 8 : 2 (1963) pp. 129–155 |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
Related to the transformations above are the Edgeworth expansions (see, e.g., [a1]; cf. also Edgeworth series).
References
| [a1] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
Random variables, transformations of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_variables,_transformations_of&oldid=28561