Difference between revisions of "Random field"
Ulf Rehmann (talk | contribs) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0773001.png | ||
| + | $#A+1 = 43 n = 1 | ||
| + | $#C+1 = 43 : ~/encyclopedia/old_files/data/R077/R.0707300 Random field, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | {| | + | {{TEX|auto}} |
| − | + | {{TEX|done}} | |
| − | |||
| − | |||
| − | |||
| − | |} | ||
| − | + | ''stochastic process in multi-dimensional time, stochastic process with a multi-dimensional parameter'' | |
| + | A [[Random function|random function]] defined on a set of points in a multi-dimensional space. Random fields are an important example of random functions (cf. [[Random element|Random element]]), which are often encountered in various applications. Some examples of random fields depending on three spatial coordinates $ x , y , z $( | ||
| + | as well as on the time $ t $) | ||
| + | are the fields of components of the velocity, of the pressure and of the temperature of a turbulent fluid flow (see [[#References|[1]]]). An example of a random field depending on two coordinates $ x $ | ||
| + | and $ y $ | ||
| + | is the height $ z $ | ||
| + | of a wavy sea surface, or the surface of any rough plate (see [[#References|[2]]]). In the investigation of global atmospheric processes on an Earth scale, the field of ground pressure and other meteorological characteristics are sometimes regarded as random fields on a sphere, etc. | ||
| − | + | The theory of random fields of a general form is almost identical with the general theory of random functions. One can only obtain more interesting concrete results for various special classes of random fields with additional properties that facilitate their study. One such class is that of homogeneous random fields (cf. [[Random field, homogeneous|Random field, homogeneous]]), defined on a homogeneous space $ S $ | |
| − | + | with a group of transformations $ G $ | |
| − | + | and having the property that the probability distributions of the values of the field on an arbitrary finite group of points of $ S $, | |
| − | + | or the mean value of the field and the second moments of its values on pairs of points, are invariant under the action of elements of $ G $ | |
| − | + | on their arguments. Homogeneous random fields on a Euclidean space $ \mathbf R ^ {k} $, | |
| − | + | $ k = 1 , 2 \dots $ | |
| + | or on the lattice $ \mathbf Z ^ {k} $ | ||
| + | of points of $ \mathbf R ^ {k} $ | ||
| + | with integral coordinates, where $ G $ | ||
| + | is the group of all possible (or all integral) parallel translations, are natural generalizations of stationary stochastic processes (cf. [[Stationary stochastic process|Stationary stochastic process]]), and many results that hold for such processes carry over in a simple way. Of great interest for applications (in particular, for the mechanics of turbulence, see [[#References|[1]]]) are the so-called homogeneous isotropic random fields on $ \mathbf R ^ {3} $ | ||
| + | and $ \mathbf R ^ {2} $, | ||
| + | where $ G $ | ||
| + | is the group of isometric transformations of the corresponding space. An important feature of homogeneous random fields is the existence of a spectral decomposition of special form, both of the fields themselves and of their correlation functions (see, for example, [[#References|[3]]], [[#References|[4]]], ; see also [[Spectral decomposition of a random function|Spectral decomposition of a random function]]). | ||
| − | + | Another class of random fields that has attracted considerable attention is that of Markov random fields, defined in some domain $ K $ | |
| + | of $ \mathbf R ^ {k} $. | ||
| + | The condition for a random field $ U ( \mathbf x ) $ | ||
| + | of being Markov asserts, roughly speaking, that for a sufficiently large family of open sets $ Q $ | ||
| + | with boundary $ \Gamma $, | ||
| + | fixing the values taken by the field in the $ \epsilon $- | ||
| + | neighbourhood $ \Gamma ^ \epsilon $ | ||
| + | of $ \Gamma $ | ||
| + | for any $ \epsilon > 0 $ | ||
| + | gives that the families of random variables $ \{ {U ( x) } : {x \in Q \setminus \Gamma ^ \epsilon } \} $ | ||
| + | and $ \{ {U ( x) } : {x \in T \setminus \Gamma ^ \epsilon } \} $, | ||
| + | where $ T $ | ||
| + | is the complement of the closure of $ Q $ | ||
| + | in $ K $, | ||
| + | are mutually independent (or, in the case of the Markov property in the wide sense, mutually uncorrelated; see, for example, [[#References|[5]]]). This can be generalized to the concept of $ L $- | ||
| + | Markov random fields, where the above independence (or orthogonality) need only hold when the $ \epsilon $- | ||
| + | neighbourhood $ \Gamma ^ \epsilon $ | ||
| + | of arbitrary width is replaced by a special type of thickened boundary $ \Gamma + L $. | ||
| + | The theory of Markov random fields and $ L $- | ||
| + | Markov fields has a number of important applications in quantum field theory and statistical physics (see [[#References|[6]]], [[#References|[7]]]). Another class of random fields arising from problems of statistical physics is that of Gibbs random fields, whose probability distributions can be expressed as Gibbs distributions (cf. [[Gibbs distribution|Gibbs distribution]]; see e.g. [[#References|[7]]], [[#References|[8]]], [[#References|[10]]]). A convenient way of defining Gibbs random fields involves a family of conditional probability distributions of values of the field in a finite domain corresponding to all its fixed values outside this domain. It must be noted that it is often convenient to regard random fields on a smooth manifold $ S $ | ||
| + | as a special case of generalized random fields, for which there may not exist values at one specified point, but the smoothened values $ U ( \phi ) $ | ||
| + | can be interpreted as random linear functionals defined on some space $ D $ | ||
| + | of smooth test functions $ \phi ( \mathbf x ) $. | ||
| + | Generalized random fields (and especially generalized Markov random fields) are widely used in physical applications. By considering within the limits of the theory of generalized random fields (cf. [[Random field, generalized|Random field, generalized]]) the fields $ U( \phi ) $, | ||
| + | where the $ \phi ( \mathbf x ) $ | ||
| + | are such that | ||
| − | + | $$ | |
| − | + | \int\limits \phi ( \mathbf x ) d \mathbf x = 0 , | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
$$ | $$ | ||
| − | |||
| − | |||
| − | |||
| + | it is also possible to define the concepts of the locally homogeneous (and locally homogeneous and locally isotropic) random fields related to stochastic processes with stationary increments (cf. [[Stochastic process with stationary increments|Stochastic process with stationary increments]]); see [[#References|[10]]], . Such fields play an important role in the statistical theory of turbulence (see, for example, [[#References|[1]]], [[#References|[9]]]). | ||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.S. Monin, A.M. Yaglom, "Statistical fluid mechanics" , '''1–2''' , M.I.T. (1971–1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.P. Khusu, Yu.R. Vitenberg, V.A. Pal'mov, "Surface roughness (a probabilistic approach)" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.J. Hannan, "Group representations and applied probability" , Methuen (1965)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.I. Yadrenko, "Spectral theory of random fields" , Optim. Software (1983) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.A. Rozanov, "Markov random fields" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730046.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> K. Preston, "Gibbs states on countable sets" , Cambridge Univ. Press (1974)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , ''Multi-component random systems'' , M. Dekker (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1990) (Translated from Russian)</TD></TR></table> | ||
| − | + | ====Comments==== | |
| − | + | For Gibbs and Markov fields see also [[#References|[a2]]]–[[#References|[a3]]]. The estimation theory of random fields is discussed in [[#References|[a4]]]–[[#References|[a5]]]. For limit theorems concerning random fields cf. [[#References|[a5]]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====References==== | ====References==== | ||
| − | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Adler, "The geometry of random fields" , Wiley (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Non standard methods in stochastic analysis and mathematical physics" , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.-O. Georgii, "Gibbs measures and phase transitions" , de Gruyter (1988)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.G. Ramm, "Random fields: estimation theory" , Longman & Wiley (1990)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.V. Ivanov, N.N. Leonenko, "Statistical analysis of random fields" , Kluwer (1989) (Translated from Russian)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | |||
Latest revision as of 08:09, 6 June 2020
stochastic process in multi-dimensional time, stochastic process with a multi-dimensional parameter
A random function defined on a set of points in a multi-dimensional space. Random fields are an important example of random functions (cf. Random element), which are often encountered in various applications. Some examples of random fields depending on three spatial coordinates $ x , y , z $( as well as on the time $ t $) are the fields of components of the velocity, of the pressure and of the temperature of a turbulent fluid flow (see [1]). An example of a random field depending on two coordinates $ x $ and $ y $ is the height $ z $ of a wavy sea surface, or the surface of any rough plate (see [2]). In the investigation of global atmospheric processes on an Earth scale, the field of ground pressure and other meteorological characteristics are sometimes regarded as random fields on a sphere, etc.
The theory of random fields of a general form is almost identical with the general theory of random functions. One can only obtain more interesting concrete results for various special classes of random fields with additional properties that facilitate their study. One such class is that of homogeneous random fields (cf. Random field, homogeneous), defined on a homogeneous space $ S $ with a group of transformations $ G $ and having the property that the probability distributions of the values of the field on an arbitrary finite group of points of $ S $, or the mean value of the field and the second moments of its values on pairs of points, are invariant under the action of elements of $ G $ on their arguments. Homogeneous random fields on a Euclidean space $ \mathbf R ^ {k} $, $ k = 1 , 2 \dots $ or on the lattice $ \mathbf Z ^ {k} $ of points of $ \mathbf R ^ {k} $ with integral coordinates, where $ G $ is the group of all possible (or all integral) parallel translations, are natural generalizations of stationary stochastic processes (cf. Stationary stochastic process), and many results that hold for such processes carry over in a simple way. Of great interest for applications (in particular, for the mechanics of turbulence, see [1]) are the so-called homogeneous isotropic random fields on $ \mathbf R ^ {3} $ and $ \mathbf R ^ {2} $, where $ G $ is the group of isometric transformations of the corresponding space. An important feature of homogeneous random fields is the existence of a spectral decomposition of special form, both of the fields themselves and of their correlation functions (see, for example, [3], [4], ; see also Spectral decomposition of a random function).
Another class of random fields that has attracted considerable attention is that of Markov random fields, defined in some domain $ K $ of $ \mathbf R ^ {k} $. The condition for a random field $ U ( \mathbf x ) $ of being Markov asserts, roughly speaking, that for a sufficiently large family of open sets $ Q $ with boundary $ \Gamma $, fixing the values taken by the field in the $ \epsilon $- neighbourhood $ \Gamma ^ \epsilon $ of $ \Gamma $ for any $ \epsilon > 0 $ gives that the families of random variables $ \{ {U ( x) } : {x \in Q \setminus \Gamma ^ \epsilon } \} $ and $ \{ {U ( x) } : {x \in T \setminus \Gamma ^ \epsilon } \} $, where $ T $ is the complement of the closure of $ Q $ in $ K $, are mutually independent (or, in the case of the Markov property in the wide sense, mutually uncorrelated; see, for example, [5]). This can be generalized to the concept of $ L $- Markov random fields, where the above independence (or orthogonality) need only hold when the $ \epsilon $- neighbourhood $ \Gamma ^ \epsilon $ of arbitrary width is replaced by a special type of thickened boundary $ \Gamma + L $. The theory of Markov random fields and $ L $- Markov fields has a number of important applications in quantum field theory and statistical physics (see [6], [7]). Another class of random fields arising from problems of statistical physics is that of Gibbs random fields, whose probability distributions can be expressed as Gibbs distributions (cf. Gibbs distribution; see e.g. [7], [8], [10]). A convenient way of defining Gibbs random fields involves a family of conditional probability distributions of values of the field in a finite domain corresponding to all its fixed values outside this domain. It must be noted that it is often convenient to regard random fields on a smooth manifold $ S $ as a special case of generalized random fields, for which there may not exist values at one specified point, but the smoothened values $ U ( \phi ) $ can be interpreted as random linear functionals defined on some space $ D $ of smooth test functions $ \phi ( \mathbf x ) $. Generalized random fields (and especially generalized Markov random fields) are widely used in physical applications. By considering within the limits of the theory of generalized random fields (cf. Random field, generalized) the fields $ U( \phi ) $, where the $ \phi ( \mathbf x ) $ are such that
$$ \int\limits \phi ( \mathbf x ) d \mathbf x = 0 , $$
it is also possible to define the concepts of the locally homogeneous (and locally homogeneous and locally isotropic) random fields related to stochastic processes with stationary increments (cf. Stochastic process with stationary increments); see [10], . Such fields play an important role in the statistical theory of turbulence (see, for example, [1], [9]).
References
| [1] | A.S. Monin, A.M. Yaglom, "Statistical fluid mechanics" , 1–2 , M.I.T. (1971–1975) (Translated from Russian) |
| [2] | A.P. Khusu, Yu.R. Vitenberg, V.A. Pal'mov, "Surface roughness (a probabilistic approach)" , Moscow (1975) (In Russian) |
| [3] | E.J. Hannan, "Group representations and applied probability" , Methuen (1965) |
| [4] | M.I. Yadrenko, "Spectral theory of random fields" , Optim. Software (1983) (Translated from Russian) |
| [5] | Yu.A. Rozanov, "Markov random fields" , Springer (1982) (Translated from Russian) |
| [6] | B. Simon, "The 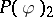 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [7] | K. Preston, "Gibbs states on countable sets" , Cambridge Univ. Press (1974) |
| [8] | R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , Multi-component random systems , M. Dekker (1980) (Translated from Russian) |
| [9] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
| [10] | V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1990) (Translated from Russian) |
Comments
For Gibbs and Markov fields see also [a2]–[a3]. The estimation theory of random fields is discussed in [a4]–[a5]. For limit theorems concerning random fields cf. [a5].
References
| [a1] | J. Adler, "The geometry of random fields" , Wiley (1981) |
| [a2] | S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Non standard methods in stochastic analysis and mathematical physics" , Acad. Press (1986) |
| [a3] | H.-O. Georgii, "Gibbs measures and phase transitions" , de Gruyter (1988) |
| [a4] | A.G. Ramm, "Random fields: estimation theory" , Longman & Wiley (1990) |
| [a5] | A.V. Ivanov, N.N. Leonenko, "Statistical analysis of random fields" , Kluwer (1989) (Translated from Russian) |
Random field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_field&oldid=38477