Ramsey theorem
The name of several theorems in discrete mathematics formulated and proved by F.P. Ramsey [1].
The first of these theorems was formulated by Ramsey as follows. Let  be an infinite class and let
be an infinite class and let  and
and  be positive integers; let all the subclasses of
be positive integers; let all the subclasses of  which have
which have  elements, in other words, all the
elements, in other words, all the  -tuples of
-tuples of  , be separated in some way into
, be separated in some way into  disjoint classes
disjoint classes  ,
,  , so that each
, so that each  -tuple is an element of one and only one class
-tuple is an element of one and only one class  ; then, assuming the axiom of choice, the class
; then, assuming the axiom of choice, the class  must contain an infinite subclass
must contain an infinite subclass  such that all the
such that all the  -tuples of
-tuples of  belong to the same class
belong to the same class  . The finite analogue of this Ramsey theorem was also established by Ramsey and can be formulated in the following way.
. The finite analogue of this Ramsey theorem was also established by Ramsey and can be formulated in the following way.
Let  be a set containing
be a set containing  elements and let
elements and let 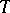 be the family of all subsets of
be the family of all subsets of  containing precisely
containing precisely  elements of
elements of  . Let the family
. Let the family  be decomposed into
be decomposed into  (non-intersecting) subfamilies
(non-intersecting) subfamilies  and let
and let  be integers,
be integers,  ,
,  . Then there exists a minimal number
. Then there exists a minimal number  , depending only on
, depending only on  and not depending on
and not depending on  , such that if
, such that if 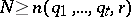 , then for some
, then for some  ,
,  , there exists a subset
, there exists a subset  of
of  with
with  elements which has all its
elements which has all its  -subsets in the family
-subsets in the family  (a proof of this theorem is also contained in [2], [3]).
(a proof of this theorem is also contained in [2], [3]).
The latter theorem can be illustrated by an example in which the number  is calculated. Consider six points in the plane which are connected in pairs by edges, each of which is coloured either red or blue. Then three points exist such that the edges joining them are coloured by the same colour. From the five edges joining a certain point
is calculated. Consider six points in the plane which are connected in pairs by edges, each of which is coloured either red or blue. Then three points exist such that the edges joining them are coloured by the same colour. From the five edges joining a certain point  with the five other points there are three edges of one colour (for example, red). Let these be the edges
with the five other points there are three edges of one colour (for example, red). Let these be the edges  ,
,  ,
,  . If one of the edges
. If one of the edges  ,
,  ,
,  is red, then it and the two others joining its ends with the point
is red, then it and the two others joining its ends with the point  form a red triangle, if they are all blue, then they themselves form a blue triangle. This means that
form a red triangle, if they are all blue, then they themselves form a blue triangle. This means that  . However, five points on the plane can be joined in pairs by red and blue edges so that no triangle of one colour can be found. To do this, let the edges
. However, five points on the plane can be joined in pairs by red and blue edges so that no triangle of one colour can be found. To do this, let the edges  ,
,  ,
,  ,
,  ,
, 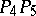 be red and the remaining blue. This shows that
be red and the remaining blue. This shows that  . Thus
. Thus  .
.
Ramsey's theorem implies the following result: For a given integer  there exists an integer
there exists an integer  such that among any
such that among any  points in the plane, no three of each lying on the same line, there are
points in the plane, no three of each lying on the same line, there are  points forming a convex
points forming a convex  -gon (see [4]).
-gon (see [4]).
References
| [1] | F.P. Ramsey, "On a problem of formal logic" Proc. London Math. Soc. Ser. 2 , 30 (1930) pp. 264–285 |
| [2] | H.J. Ryser, "Combinatorial mathematics" , Math. Assoc. Amer. (1963) |
| [3] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
| [4] | P. Erdös, G. Szekeres, "A combinatorial problem in geometry" Compos. Math. , 2 (1935) pp. 463–470 |
| [5] | P. Erdös, R. Rado, "A partition calculus in set theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 427–489 |
Comments
Nowadays, the study of Ramsey-like theorems has grown into a separate branch of combinatorics, called Ramsey theory.
References
| [a1] | R.L. Graham, B.L. Rothschild, J.H. Spencer, "Ramsey theory" , Wiley (1980) |
| [a2] | P. Erdös, A. Hajnal, A. Mate, R. Rado, "Combinatorial set theory: partition relations for cardinals" , North-Holland (1984) |
Ramsey theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ramsey_theorem&oldid=17790