Ramanujan hypothesis
From Encyclopedia of Mathematics
Ramanujan conjecture
The conjecture, stated by S. Ramanujan [1], that the Fourier coefficients 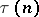 of the function
of the function 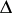 (a cusp form of weight 12) satisfy the inequality
(a cusp form of weight 12) satisfy the inequality
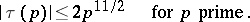 |
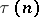 is also called the Ramanujan function. The function
is also called the Ramanujan function. The function 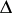 is an eigen function of the Hecke operator, and the
is an eigen function of the Hecke operator, and the 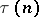 are the corresponding eigen values. H. Petersson generalized Ramanujan's hypothesis to the case of eigen values of the Hecke operators on modular forms of weight
are the corresponding eigen values. H. Petersson generalized Ramanujan's hypothesis to the case of eigen values of the Hecke operators on modular forms of weight 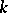 ,
, 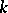 an integer
an integer 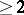 (the Petersson conjecture). P. Deligne (see [2]) reduced the Petersson conjecture to the Weil conjectures (cf. Zeta-function), then proved the latter (1974). This also proved Ramanujan's hypothesis.
(the Petersson conjecture). P. Deligne (see [2]) reduced the Petersson conjecture to the Weil conjectures (cf. Zeta-function), then proved the latter (1974). This also proved Ramanujan's hypothesis.
References
| [1] | S. Ramanujan, "On certain arithmetical functions" Trans. Cambridge Philos. Soc. , 22 (1916) pp. 159–184 |
| [2] | P. Deligne, "La conjecture de Weil 1" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [3] | O.M. Fomenko, "Applications of the theory of modular forms to number theory" J. Soviet Math. , 14 : 4 (1980) pp. 1307–1362 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 15 (1977) pp. 5–91 |
Comments
See also Congruence equation.
References
| [a1] | N.M. Katz, "An overview of Deligne's proof of the Riemann hypothesis for varieties over finite fields" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 275–305 |
How to Cite This Entry:
Ramanujan hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ramanujan_hypothesis&oldid=12288
Ramanujan hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ramanujan_hypothesis&oldid=12288
This article was adapted from an original article by K.Yu. Bulota (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article