Radon transform
An integral transform of a function in several variables, related to the Fourier transform. It was introduced by J. Radon (see [1]).
Let  be a continuous function of the real variables
be a continuous function of the real variables  that is decreasing sufficiently rapidly at infinity,
that is decreasing sufficiently rapidly at infinity,  ,
,  .
.
For any hyperplane in  ,
,
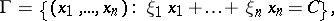 |
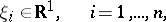 |
and
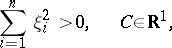 |
the following integral is defined:
 |
where 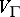 is the Euclidean
is the Euclidean 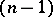 -dimensional volume in the hyperplane
-dimensional volume in the hyperplane 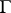 . The function
. The function
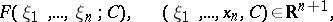 |
is called the Radon transform of the function  . It is a homogeneous function of its variables of degree
. It is a homogeneous function of its variables of degree 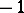 :
:
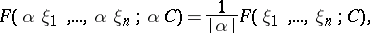 |
and is related to the Fourier transform 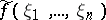 ,
, 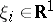 , of
, of 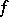 by
by
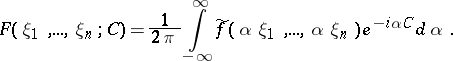 |
The Radon transform is immediately associated with the problem, going back to Radon, of the recovery of a function 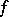 from the values of its integrals calculated over all hyperplanes of the space
from the values of its integrals calculated over all hyperplanes of the space  (that is, the problem of the inversion of the Radon transform).
(that is, the problem of the inversion of the Radon transform).
References
| [1] | J. Radon, "Ueber die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten" Ber. Verh. Sächs. Akad. , 69 (1917) pp. 262–277 |
| [2] | I.M. Gel'fand, M.I. Graev, N.Ya. Vilenkin, "Generalized functions" , 5. Integral geometry and representation theory , Acad. Press (1966) (Translated from Russian) |
Comments
For the far-reaching generalizations of the Radon transform to homogeneous spaces see [a3].
The Radon transform and, in particular, the corresponding inversion formula (i.e. the formula recovering 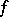 from its Radon transform) is of central importance in tomography.
from its Radon transform) is of central importance in tomography.
References
| [a1] | S.R. Deans, "The Radon transform and some of its applications" , Wiley (1983) |
| [a2] | S. Helgason, "The Radon transform" , Birkhäuser (1980) |
| [a3] | S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4 |
Radon transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radon_transform&oldid=14894