Radon measure

inner regular measure

A finite measure 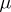(cf. Measure in a topological vector space) defined on the Borel 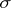-algebra 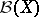of a topological space 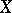, and having the following property: For any 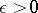there is a compactum 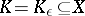such that 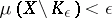. It was introduced by J. Radon (1913), whose original constructions referred to measures on the 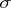-algebra 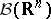, the Borel 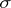-algebra of the space 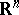, 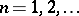. A topological space 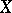is called a Radon space if every finite measure defined on the 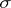-algebra 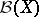is a Radon measure.

References

[1]	N. Bourbaki, "Eléments de mathématiques. Intégration" , Hermann (1963) pp. Chapts. 6 - 8
[2]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)

Comments

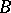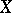Any Radon measure is tight (also called inner regular): For any Borel subset of one has

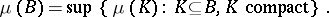If 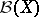is countably generated, 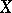is a Radon space if and only if it is Borel isomorphic to a universally measurable subset of 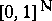(or any other uncountable compact metrizable space). In particular, any polish space, or more generally Suslin space in the sense of Bourbaki, is Radon.

One can also define non-finite (non-negative) Radon measures; they are tight and take finite values on compact subsets. If 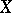has a countable basis, they are 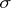-finite.

Following N. Bourbaki (and ideas going back to W.H. Young and Ch. de la Vallée-Poussin), a (non-negative) Radon measure on, say, a locally compact space 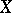is a (non-negative) continuous linear functional on the space 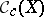of continuous functions with compact support endowed with its natural inductive topology. One can prove with the help of the Riesz–Markov theorem (which deals with the case 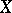compact) that any non-negative and bounded Radon measure in this sense is the restriction to of the integral with respect to a unique (finite) Radon measure as defined in the article above; the converse is true and trivial.