Radon-Nikodým theorem
A charge  that is absolutely continuous with respect to some measure
that is absolutely continuous with respect to some measure 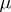 has a density
has a density 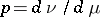 with respect to
with respect to 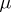 that is summable with respect to this measure. It was established by J. Radon [1] and O.M. Nikodým [2]. More precisely, on a measurable space
that is summable with respect to this measure. It was established by J. Radon [1] and O.M. Nikodým [2]. More precisely, on a measurable space 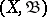 , where
, where 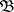 is a
is a 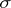 -algebra of subsets of
-algebra of subsets of 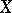 , suppose one is given a charge
, suppose one is given a charge  , i.e. a countably-additive real or complex function given on
, i.e. a countably-additive real or complex function given on 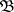 , and a
, and a 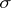 -finite measure
-finite measure 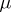 , and, moreover, let
, and, moreover, let  be absolutely continuous with respect to
be absolutely continuous with respect to 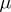 . Then there is a function
. Then there is a function 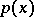 ,
,  , summable with respect to
, summable with respect to 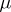 , such that for any set
, such that for any set 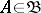 ,
,
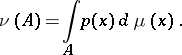 |
The function 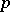 is unique (except for modifications on a set of
is unique (except for modifications on a set of 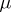 -measure zero), and is called the density of the charge
-measure zero), and is called the density of the charge  with respect to the measure
with respect to the measure 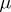 . There are (see [4]) generalizations of the theorem to the case when the charge takes values in some vector space.
. There are (see [4]) generalizations of the theorem to the case when the charge takes values in some vector space.
References
| [1] | J. Radon, "Ueber lineare Funktionaltransformationen und Funktionalgleichungen" Sitzungsber. Acad. Wiss. Wien , 128 (1919) pp. 1083–1121 |
| [2] | O.M. Nikodým, "Sur une généralisation des intégrales de M. J. Radon" Fund. Math. , 15 (1930) pp. 131–179 |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [4] | J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) |
Comments
The notion of "charge" is not well established in the West; one usually says "signed measure" (cf. Charge). The density 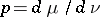 is also well defined if
is also well defined if  is the sum of a series of (non-negative) measures; in this case
is the sum of a series of (non-negative) measures; in this case 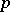 and the integral may take the value
and the integral may take the value 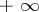 .
.
The theorem is false if 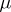 fails to satisfy same finiteness condition; see [a1], §19, for a thorough discussion and illuminating examples.
fails to satisfy same finiteness condition; see [a1], §19, for a thorough discussion and illuminating examples.
For the generalizations of the theorem to vector measures (and relations to the geometry of Banach spaces) see Vector measure.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Radon-Nikodým theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radon-Nikod%C3%BDm_theorem&oldid=15021