Radial boundary value
The value of a function  , defined on the unit disc
, defined on the unit disc  , at a boundary point
, at a boundary point  , equal to the limit
, equal to the limit
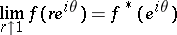 |
of the function  on the set of points of the radius
on the set of points of the radius  leading to the point
leading to the point  . The term "radial boundary value" is sometimes used in a generalized sense for functions
. The term "radial boundary value" is sometimes used in a generalized sense for functions  given on arbitrary (including multi-dimensional) domains
given on arbitrary (including multi-dimensional) domains  , where
, where  is taken to be the set of points of a normal (or its analogue) to the boundary of
is taken to be the set of points of a normal (or its analogue) to the boundary of  leading to the boundary point. For example, in the case of a bi-disc
leading to the boundary point. For example, in the case of a bi-disc
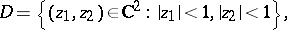 |
as the radial boundary value at 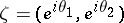 one takes the limit
one takes the limit
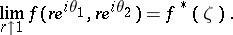 |
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
The functions under consideration are usually analytic or harmonic functions. See also Boundary properties of analytic functions and its references; cf. also Angular boundary value; and Fatou theorem.
Radial boundary value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radial_boundary_value&oldid=15727