Quotient group
of a group 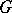 by a normal subgroup
by a normal subgroup 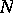
The group formed by the cosets (cf. Coset in a group) 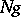 ,
, 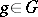 , of
, of 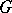 ; it is denoted by
; it is denoted by 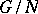 (cf. Normal subgroup). Multiplication of cosets is performed according to the formula
(cf. Normal subgroup). Multiplication of cosets is performed according to the formula
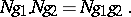 |
The unit of the quotient group is the coset 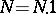 , and the inverse of the coset
, and the inverse of the coset 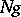 is
is 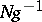 .
.
The mapping 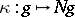 is a group epimorphism of
is a group epimorphism of 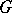 onto
onto 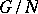 , called the canonical epimorphism or natural epimorphism. If
, called the canonical epimorphism or natural epimorphism. If 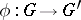 is an arbitrary epimorphism of
is an arbitrary epimorphism of 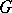 onto a group
onto a group 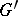 , then the kernel
, then the kernel 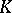 of
of 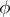 is a normal subgroup of
is a normal subgroup of 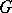 , and the quotient group
, and the quotient group 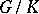 is isomorphic to
is isomorphic to 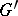 ; more precisely, there is an isomorphism
; more precisely, there is an isomorphism 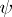 of
of 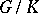 onto
onto 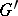 such that the diagram
such that the diagram
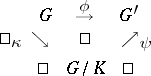 |
is commutative, where 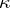 is the natural epimorphism
is the natural epimorphism 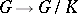 .
.
A quotient group of a group 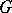 can be defined, starting from some congruence on
can be defined, starting from some congruence on 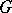 (cf. Congruence (in algebra)), as the set of classes of congruent elements relative to multiplication of classes. All possible congruences on a group are in one-to-one correspondence with its normal subgroups, and the quotient groups by the congruences are the same as those by the normal subgroups. A quotient group is a normal quotient object in the category of groups.
(cf. Congruence (in algebra)), as the set of classes of congruent elements relative to multiplication of classes. All possible congruences on a group are in one-to-one correspondence with its normal subgroups, and the quotient groups by the congruences are the same as those by the normal subgroups. A quotient group is a normal quotient object in the category of groups.
Comments
References
| [a1] | P.M. Cohn, "Algebra" , I , Wiley (1982) pp. Sect. 9.1 |
Quotient group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quotient_group&oldid=16178