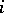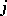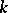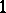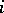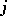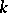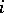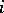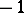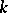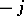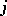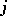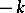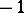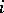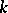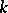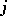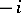Quaternion
A hypercomplex number, geometrically realizable in four-dimensional space. The system of quaternions was put forward in 1843 by W.R. Hamilton (1805–1865). Quaternions were historically the first example of a hypercomplex system, arising from attempts to find a generalization of complex numbers. Complex numbers are depicted geometrically by points in the plane and operations on them correspond to the simplest geometric transformations of the plane. It is not possible to "organize" a number system similar to the field of real or complex numbers from the points of a space of three or more dimensions. However, if one drops the requirement of commutativity of multiplication, then it is possible to construct a number system from the points of 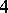 -dimensional space. (In 3, 5 or higher-dimensional space it is not even possible to do this.)
-dimensional space. (In 3, 5 or higher-dimensional space it is not even possible to do this.)
The quaternions form a 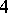 -dimensional algebra over the field of real numbers with basis
-dimensional algebra over the field of real numbers with basis 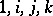 ( "basic units" ) and the following multiplication table of the "basic units" :'
( "basic units" ) and the following multiplication table of the "basic units" :'
<tbody> </tbody>
|
Every quaternion can be written in the form
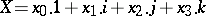 |
or (since 1 plays the role of ordinary identity and in writing a quaternion it can be omitted) in the form
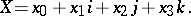 |
One distinguishes the scalar part 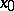 of the quaternion and its vector part
of the quaternion and its vector part
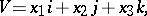 |
so that 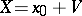 . If
. If  , then the quaternion
, then the quaternion 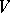 is called a vector and can be identified with an ordinary
is called a vector and can be identified with an ordinary  -dimensional vector, since multiplication in the algebra of quaternions of two such vectors
-dimensional vector, since multiplication in the algebra of quaternions of two such vectors 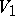 and
and 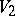 is related to the scalar and vector products
is related to the scalar and vector products 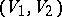 (cf. Inner product) and
(cf. Inner product) and 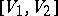 (cf. Vector product) of the vectors
(cf. Vector product) of the vectors 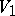 and
and 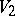 in
in  -dimensional space by the formula
-dimensional space by the formula
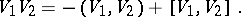 |
This shows the close relationship between quaternions and vector calculus. Historically, the latter arose from the theory of quaternions.
Corresponding to each quaternion 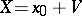 is the conjugate quaternion
is the conjugate quaternion 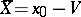 , and
, and
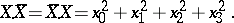 |
This real number is called the norm of the quaternion 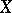 and is denoted by
and is denoted by 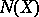 . This norm satisfies the relation
. This norm satisfies the relation
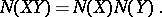 |
Any rotation of  -dimensional space about the origin can be defined by means of a quaternion
-dimensional space about the origin can be defined by means of a quaternion 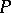 with norm 1. The rotation corresponding to
with norm 1. The rotation corresponding to 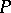 takes the vector
takes the vector 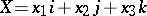 to the vector
to the vector 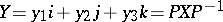 .
.
The algebra of quaternions is the unique associative non-commutative finite-dimensional normed algebra over the field of real numbers with an identity. The algebra of quaternions is a skew-field, that is, division is defined in it, and the quaternion inverse to a quaternion 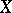 is
is 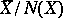 . The skew-field of quaternions is the unique finite-dimensional real associative non-commutative algebra without divisors of zero (see also Frobenius theorem; Cayley–Dickson algebra).
. The skew-field of quaternions is the unique finite-dimensional real associative non-commutative algebra without divisors of zero (see also Frobenius theorem; Cayley–Dickson algebra).
References
| [1] | L.A. Kaluzhnin, "Introduction to general algebra" , Moscow (1973) (In Russian) |
| [2] | I.L. Kantor, A.S. Solodovnikov, "Hyperkomplexe Zahlen" , Teubner (1978) (Translated from Russian) |
| [3] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
Let 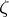 be the element
be the element 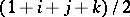 in the algebra of quaternions. The Hurwitz ring of integral quaternions is the ring
in the algebra of quaternions. The Hurwitz ring of integral quaternions is the ring
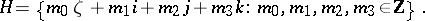 |
The Hurwitz ring is a non-commutative ring in which an analogue of the Euclidean division property (cf. Euclidean algorithm) holds: For any 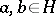 with
with 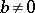 there exist elements
there exist elements 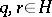 such that
such that
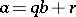 |
with
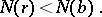 |
(This property does not hold for the subring 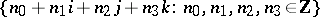 .) It follows that every left ideal is left principal, and this in turn can be used to give a proof of the Lagrange four-square theorem, to the effect that every positive integer can be written as a sum of four squares of integers.
.) It follows that every left ideal is left principal, and this in turn can be used to give a proof of the Lagrange four-square theorem, to the effect that every positive integer can be written as a sum of four squares of integers.
The Lagrange identity, which plays an important role in the proof of this result,
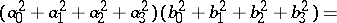 |
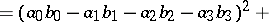 |
 |
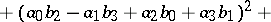 |
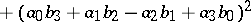 |
for real numbers 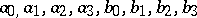 , is equivalent to the multiplicativity of the norm
, is equivalent to the multiplicativity of the norm 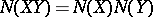 , where
, where 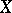 ,
, 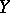 are the quaternions
are the quaternions 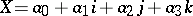 ,
, 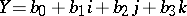 .
.
Writing 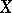 as
as 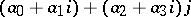 and putting
and putting 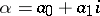 ,
, 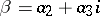 , one obtains
, one obtains 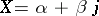 . It is easily proved that the algebra of quaternions is isomorphic to the algebra of complex
. It is easily proved that the algebra of quaternions is isomorphic to the algebra of complex 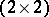 -matrices
-matrices
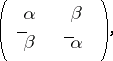 |
with 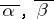 the complex conjugates of
the complex conjugates of 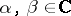 .
.
When one wishes to retain the multiplicativity of the norm, 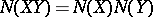 , there is only one possible generalization of the quaternions (over the reals): the octaves or octonions, which have 8 instead of 4 components (Hurwitz's theorem, 1898; cf. Cayley numbers).
, there is only one possible generalization of the quaternions (over the reals): the octaves or octonions, which have 8 instead of 4 components (Hurwitz's theorem, 1898; cf. Cayley numbers).
The centre of the skew-field of quaternions is the field of real numbers. Later the notion of hypercomplex system has been generalized in a theory of skew-fields over arbitrary fields, e.g. the theory of the Brauer group of a commutative field.
In this connection, a generalized quaternion algebra is a 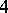 -dimensional algebra over a field
-dimensional algebra over a field 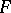 generated by
generated by 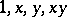 with multiplication table
with multiplication table 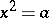 ,
, 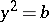 ,
, 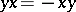 , where
, where 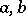 are non-zero elements of
are non-zero elements of 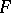 . (The quaternions are the case
. (The quaternions are the case 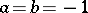 , and
, and 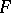 the field of real numbers.)
the field of real numbers.)
References
| [a1] | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1935) |
| [a2] | R. Brauer, E. Noether, "Über minimale Zerfällungskörper irreducibler Darstellungen" Sitzungsber. Akad. Berlin , 27 (1927) pp. 221–226 |
| [a3] | J.H.M. Wedderburn, "On hypercomplex numbers" Proc. London Math. Soc. Ser. 2 , 6 (1907) pp. 77–118 |
| [a4] | R. Brauer, E. Weiss, "Non-commutative rings" , Harvard Univ. Press (1950) pp. Part I |
| [a5] | H. Behnke, F. Bachmann, "Grundzüge der Mathematik" , I , Göttingen (1962) |
| [a6] | S. Maclane, G. Birkhoff, "Algebra" , Macmillan (1979) |
| [a7] | M. Crowe, "A history of vector analysis, the evolution of the idea of a vectorial system" , Univ. Notre Dame (1967) |
| [a8] | R.J. Stephenson, "Development of vector analysis from quaternions" Amer. J. Physics , 34 (1966) pp. 194–201 |
| [a9] | B.L. van der Waerden, "Hamiltons Entdeckung der Quaternionen" , Vandenhoeck & Ruprecht (1973) |
| [a10] | I.N. Herstein, "Topics in algebra" , Wiley (1975) pp. Sect. 7.4 |
Quaternion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quaternion&oldid=12609