Quasi-uniform convergence
From Encyclopedia of Mathematics
A generalization of uniform convergence. A sequence of mappings  from a topological space
from a topological space  into a metric space
into a metric space  converging pointwise to a mapping
converging pointwise to a mapping  is called quasi-uniformly convergent if for any
is called quasi-uniformly convergent if for any  and any positive integer
and any positive integer  there exist a countable open covering
there exist a countable open covering 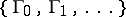 of
of  and a sequence
and a sequence  of positive integers greater than
of positive integers greater than  such that
such that  for every
for every  . Uniform convergence implies quasi-uniform convergence. For sequences of continuous functions, quasi-uniform convergence is a necessary and sufficient condition for the limit function to be continuous (the Arzelà–Aleksandrov theorem).
. Uniform convergence implies quasi-uniform convergence. For sequences of continuous functions, quasi-uniform convergence is a necessary and sufficient condition for the limit function to be continuous (the Arzelà–Aleksandrov theorem).
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
How to Cite This Entry:
Quasi-uniform convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-uniform_convergence&oldid=14862
Quasi-uniform convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-uniform_convergence&oldid=14862
This article was adapted from an original article by V.V. Fedorchuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article