Quasi-triangular Hopf algebra
dual quasi-triangular Hopf algebra, co-quasi-triangular Hopf algebra, quantum group
A quantum group in the strict sense, i.e. a Hopf algebra 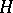 equipped with a further (co-) quasi-triangular structure
equipped with a further (co-) quasi-triangular structure 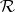 obeying certain axioms such that the category of (co-) modules of
obeying certain axioms such that the category of (co-) modules of 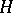 is a braided category (cf. also Quantum groups). This is arguably the key property behind the quantum group enveloping algebras
is a braided category (cf. also Quantum groups). This is arguably the key property behind the quantum group enveloping algebras 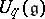 or their associated quantum group coordinate rings
or their associated quantum group coordinate rings 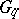 .
.
More precisely, a quasi-triangular Hopf algebra is 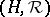 where
where 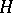 is a Hopf algebra over a field
is a Hopf algebra over a field 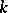 and
and 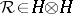 obeys
obeys
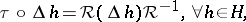 |
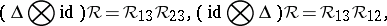 |
where  is the permutation operation on
is the permutation operation on 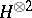 and
and 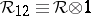 ,
, 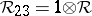 are in
are in 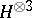 in the latter equations. One may show that
in the latter equations. One may show that  then obeys
then obeys
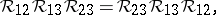 |
which is an abstract form of the Yang–Baxter equation. One denotes the Hopf algebra structure by 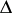 for the co-product, and denotes by
for the co-product, and denotes by  the co-unit and by
the co-unit and by 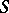 the antipode.
the antipode.
Examples.
1) When 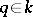 is an
is an  th root of
th root of 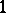 , the quantum group
, the quantum group  is given by the polynomial algebra
is given by the polynomial algebra 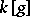 modulo
modulo 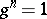 (the group ring of
(the group ring of 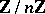 ) with co-algebra, antipode and quasi-triangular structure
) with co-algebra, antipode and quasi-triangular structure
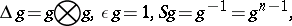 |
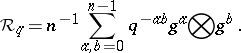 |
It is assumed that  is invertible in
is invertible in 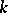 .
.
2) When 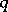 is a primitive
is a primitive  th root of
th root of 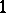 , the finite-dimensional quantum group
, the finite-dimensional quantum group 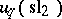 is the free associative algebra
is the free associative algebra 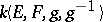 modulo the relations
modulo the relations
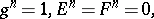 |
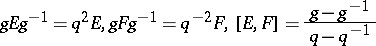 |
and the co-algebra, antipode and quasi-triangular structure
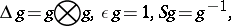 |
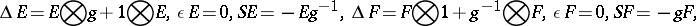 |
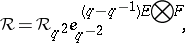 |
where
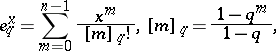 |
is the 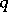 -exponential with
-exponential with 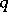 -integers
-integers 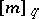 in the factorial.
in the factorial.
For general 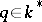 (an invertible element of
(an invertible element of 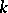 ), one has the infinite-dimensional Hopf algebra
), one has the infinite-dimensional Hopf algebra 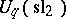 , where the
, where the 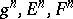 relations above are omitted. In this case
relations above are omitted. In this case 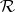 has to be described via some form of completion. One formulation is to work over the ring of formal power series
has to be described via some form of completion. One formulation is to work over the ring of formal power series 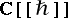 rather than over a field as above. If it is assumed that
rather than over a field as above. If it is assumed that 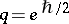 and
and 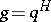 , one can reformulate
, one can reformulate 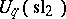 with
with 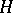 as a generator and define
as a generator and define 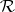 with
with 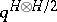 in place of
in place of 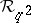 above (and now take an infinite sum in the exponential). It does not, however, live in the algebraic tensor product but in a completion of it. On the other hand, this formulation allows one to consider the structure to lowest order in
above (and now take an infinite sum in the exponential). It does not, however, live in the algebraic tensor product but in a completion of it. On the other hand, this formulation allows one to consider the structure to lowest order in 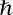 . This is the Lie algebra
. This is the Lie algebra 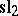 , the Lie co-bracket
, the Lie co-bracket 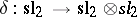 (forming a Lie bi-algebra) and a Lie quasi-triangular structure
(forming a Lie bi-algebra) and a Lie quasi-triangular structure 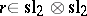 obeying the classical Yang–Baxter equations. It extends to a Poisson bracket (cf. Poisson brackets) on the group
obeying the classical Yang–Baxter equations. It extends to a Poisson bracket (cf. Poisson brackets) on the group 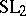 , making it a Poisson Lie group. This means a Poisson bracket on the group such that the product mapping is a Poisson mapping from the direct product Poisson structure. There are similar quantum group enveloping algebras
, making it a Poisson Lie group. This means a Poisson bracket on the group such that the product mapping is a Poisson mapping from the direct product Poisson structure. There are similar quantum group enveloping algebras 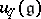 and
and 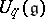 for all complex semi-simple Lie algebras
for all complex semi-simple Lie algebras  .
.
3) Every finite-dimensional Hopf algebra 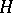 with invertible antipode can be "doubled" to obtain a quasi-triangular Hopf algebra
with invertible antipode can be "doubled" to obtain a quasi-triangular Hopf algebra 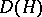 , called the quantum double of
, called the quantum double of 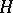 . This contains
. This contains  and
and 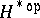 (the dual of
(the dual of 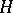 with reversed product) as sub-Hopf algebras and the additional cross relations
with reversed product) as sub-Hopf algebras and the additional cross relations
 |
for all 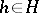 and
and 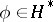 , where
, where 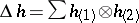 is a notation for the co-product of
is a notation for the co-product of 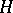 , etc., and
, etc., and 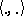 denotes the evaluation pairing. The quasi-triangular structure is
denotes the evaluation pairing. The quasi-triangular structure is
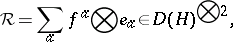 |
where 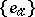 is a basis of
is a basis of 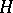 and
and 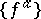 is a dual basis.
is a dual basis.  can in fact be built explicitly on the vector space
can in fact be built explicitly on the vector space 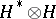 as a double cross product
as a double cross product 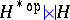 . The braided category of
. The braided category of 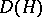 -modules can be identified with that of crossed
-modules can be identified with that of crossed 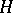 -modules
-modules  by viewing a co-action of
by viewing a co-action of 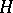 as an action of
as an action of 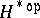 by evaluation.
by evaluation.
Dually, i.e. reversing all arrows, one has the notion of a dual quasi-triangular or co-quasi-triangular Hopf algebra 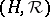 where
where 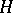 is a Hopf algebra and
is a Hopf algebra and 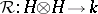 obeys
obeys
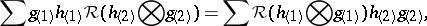 |
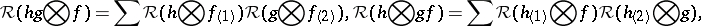 |
for 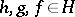 . One also requires
. One also requires 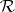 to be convolution-invertible in the sense
to be convolution-invertible in the sense
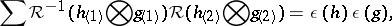 |
 |
for 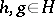 .
.
A) Let 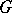 be an Abelian group equipped with a bi-character
be an Abelian group equipped with a bi-character  (a function multiplicative in each input). The group algebra
(a function multiplicative in each input). The group algebra 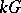 is the vector space with basis
is the vector space with basis 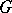 and with product among basis elements the group product. The co-product
and with product among basis elements the group product. The co-product 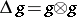 and co-unit
and co-unit 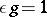 extended linearly make
extended linearly make 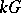 into a Hopf algebra. The bi-character makes this dual quasi-triangular, with
into a Hopf algebra. The bi-character makes this dual quasi-triangular, with 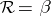 on basis elements, extended linearly.
on basis elements, extended linearly.
B) The dual quasi-triangular Hopf algebra 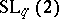 is the free associative algebra
is the free associative algebra 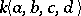 modulo the relations
modulo the relations
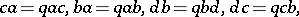 |
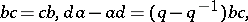 |
and the "q-determinant relation"
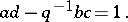 |
The co-algebra has the matrix form
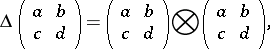 |
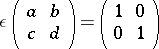 |
(matrix multiplication understood). The antipode is
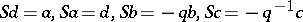 |
and the dual quasi-triangular structure is
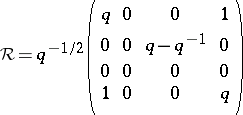 |
on a basis 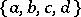 of generators. The extension to products is then determined. Here it is assumed that
of generators. The extension to products is then determined. Here it is assumed that 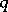 has a square root in
has a square root in 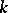 . The quantum group
. The quantum group 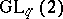 is similar, with
is similar, with 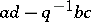 inverted rather than set to
inverted rather than set to 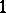 .
.
There are similar quantum group coordinate rings 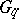 for the standard families of simple Lie groups, known explicitly for the non-exceptional families. They are deformations of the classical coordinate rings and in fact quantize the Poisson Lie group structures on
for the standard families of simple Lie groups, known explicitly for the non-exceptional families. They are deformations of the classical coordinate rings and in fact quantize the Poisson Lie group structures on 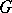 corresponding to
corresponding to 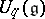 . They are dually paired as Hopf algebras with
. They are dually paired as Hopf algebras with  .
.
C) More generally, given any invertible matrix solution 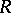 of the Yang–Baxter equations, there is a dual-quasi-triangular bi-algebra of quantum matrices
of the Yang–Baxter equations, there is a dual-quasi-triangular bi-algebra of quantum matrices 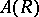 as the free associative algebra
as the free associative algebra 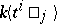 (on a matrix of generators) modulo the relations
(on a matrix of generators) modulo the relations
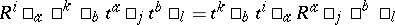 |
(summation of repeated indices). The co-algebra has the matrix form
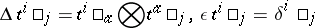 |
(summation over  ). The dual-quasi-triangular structure is
). The dual-quasi-triangular structure is
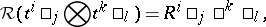 |
extended to products by the quasi-triangularity axioms. Note that 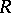 need not obey the Yang–Baxter equations in order to have a bi-algebra:
need not obey the Yang–Baxter equations in order to have a bi-algebra: 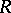 provides the dual quasi-triangular structure.
provides the dual quasi-triangular structure.
In between these formulations is an intermediate one, called a quasi-triangular dual pair. This is a pair of Hopf algebras 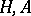 , a duality pairing
, a duality pairing 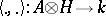 between them, and a mapping
between them, and a mapping 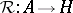 obeying certain axioms. In particular,
obeying certain axioms. In particular, 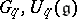 are dually paired and there is a suitable mapping
are dually paired and there is a suitable mapping 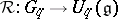 . This provides a way of working with quasi-triangular structures that includes quantum group enveloping algebras but avoids formal power series.
. This provides a way of working with quasi-triangular structures that includes quantum group enveloping algebras but avoids formal power series.
References
| [a1] | V.G. Drinfel'd, "Quantum groups" A. Gleason (ed.) , Proc. Internat. Math. Congress , Amer. Math. Soc. (1987) pp. 798–820 |
| [a2] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtajan, "Quantization of Lie groups and Lie algebras" Leningrad Math. J. , 1 (1990) pp. 193–225 |
| [a3] | S. Majid, "Quasitriangular Hopf algebras and Yang-Baxter equations" Internat. J. Modern Physics A , 5 : 1 (1990) pp. 1–91 |
| [a4] | S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995) |
Quasi-triangular Hopf algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-triangular_Hopf_algebra&oldid=15295