Quasi-norm

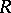A non-negative function defined on a linear space and satisfying the same axioms as a norm except for the triangle inequality 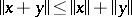, which is replaced by the weaker requirement: There exists a constant such that 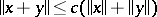for all .

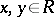Comments

The topology of a locally bounded topological vector space can be given by a quasi-norm. Conversely, a quasi-normed vector space is locally bounded. Here a set 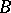in a topological vector space is bounded if for each open neighbourhood 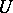of zero there is a 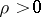such that 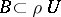, and a topological vector space is locally bounded if there is a bounded neighbourhood of zero. Given a circled bounded neighbourhood 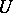of zero in a topological vector space 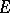(a set 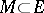is circled if 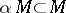for all 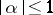), the Minkowski functional of 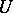is defined by 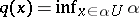. It is a quasi-norm.

References

[a1]	G. Köthe, "Topological vector spaces" , 1 , Springer (1969) pp. 159