Quasi-linearization
A collection of methods for the numerical solution of non-linear problems by reducing them to a sequence of linear problems. Lying at the basis of the apparatus of quasi-linearization is the Newton method and its generalization to function spaces, the theory of differential inequalities (cf. Differential inequality) and the method of dynamic programming. The simplest example illustrating a method of quasi-linearization is the use of the Newton–Raphson method for finding the root  of a scalar monotone-decreasing strictly-convex function
of a scalar monotone-decreasing strictly-convex function  . In case the original non-linear function
. In case the original non-linear function  is approximated at each stage of the iteration process by a linear function
is approximated at each stage of the iteration process by a linear function  , the root of
, the root of  is found, which serves as the next approximation, so that
is found, which serves as the next approximation, so that
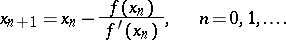 |
Under fairly general conditions the sequence so constructed has the property of monotonicity  and quadratic convergence:
and quadratic convergence:
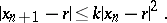 |
The application of quasi-linearization to solving the Riccati equation
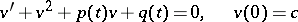 |
(it is assumed that a solution exists on an interval 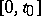 ), is as follows. The original equation is replaced by the equivalent equation
), is as follows. The original equation is replaced by the equivalent equation
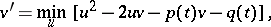 |
where the minimum is taken over all functions  defined on
defined on 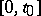 . This equation has a number of properties inherent to linear equations, and in order to solve it one uses the linear differential equation
. This equation has a number of properties inherent to linear equations, and in order to solve it one uses the linear differential equation
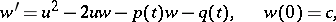 |
where  is a fixed function. By appealing to the property
is a fixed function. By appealing to the property 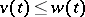 (equality holding when
(equality holding when  ), one can construct a system of successive approximations
), one can construct a system of successive approximations
 |
satisfying the linear equations
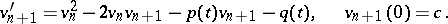 |
The same recurrence relation can be obtained by applying the Newton–Kantorovich method (cf. Kantorovich process) to the original non-linear equation.
The employment of a quasi-linearization scheme in the solution of boundary value problems for the non-linear second-order differential equation
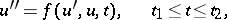 |
 |
leads to a sequence of functions 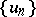 satisfying the linear equations
satisfying the linear equations
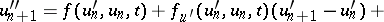 |
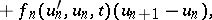 |
with the linearized boundary conditions
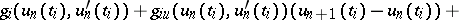 |
 |
The existence, uniqueness and quadratic convergence of the sequence follows from the corresponding convexity of the functions 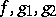 over a sufficiently small interval
over a sufficiently small interval  .
.
The method of quasi-linearization finds application in the solution of two-point and multi-point boundary value problems for linear and non-linear ordinary differential equations, boundary value problems for elliptic and parabolic partial differential equations, variational problems, differential-difference and functional-differential equations, etc. As with every iteration scheme, the method of quasi-linearization is suitable for computer implementation and has various modifications enabling one to accelerate the convergence for narrower classes of problems. There exists a variety of examples of its use as a heuristic method for solving a number of problems in physics, technology and economy.
References
| [1] | R.E. Bellman, R.E. Kalaba, "Quasilinearization and nonlinear boundary-value problems" , Elsevier (1965) (Translated from Russian) |
Comments
References
| [a1] | R. Bellman, G. Adomian, "Partial differential equations" , Reidel (1985) pp. Chapt. IV |
| [a2] | R. Bellman, R. Vasudevan, "Wave propagation. An invariant imbedding approach" , Reidel (1986) |
Quasi-linearization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-linearization&oldid=17538