Quasi-geodesic line
From Encyclopedia of Mathematics
quasi-geodesic
A curve on a surface on any segment of which the right and left rotations have the same sign (see Swerve of a curve). For example, the edge of a lens is a quasi-geodesic line.
The class of quasi-geodesic lines substantially amplifies the class of geodesic lines (cf. Geodesic line), making its families (bounded in length and position) compact. In a two-dimensional manifold 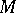 of bounded curvature there passes through each point at least one quasi-geodesic in each direction; it can always be extended. Segments of quasi-geodesics (at the ends of which there are no points of curvature
of bounded curvature there passes through each point at least one quasi-geodesic in each direction; it can always be extended. Segments of quasi-geodesics (at the ends of which there are no points of curvature 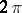 on
on 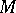 ) are limits of geodesics lying on smooth surfaces properly converging to
) are limits of geodesics lying on smooth surfaces properly converging to 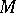 .
.
References
| [1] | A.D. Aleksandrov, Yu.D. Burago, "Quasigeodesics" Proc. Steklov Inst. Math. , 76 (1965) pp. 58–76 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 49–63 |
Comments
References
| [a1] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
How to Cite This Entry:
Quasi-geodesic line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-geodesic_line&oldid=17208
Quasi-geodesic line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-geodesic_line&oldid=17208
This article was adapted from an original article by V.A. Zalgaller (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article