Quasi-cyclic group
group of type 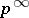
An infinite Abelian 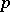 -group all proper subgroups of which are cyclic (cf. Cyclic group). There exists for each prime number
-group all proper subgroups of which are cyclic (cf. Cyclic group). There exists for each prime number 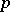 a quasi-cyclic group, and it is unique up to an isomorphism. This group is isomorphic to the multiplicative group of all roots of the equations
a quasi-cyclic group, and it is unique up to an isomorphism. This group is isomorphic to the multiplicative group of all roots of the equations
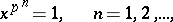 |
in the field of complex numbers with the usual multiplication, and also to the quotient group 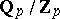 , where
, where 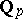 is the additive group of the field of rational
is the additive group of the field of rational 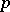 -adic numbers and
-adic numbers and 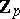 is the additive group of the ring of all
is the additive group of the ring of all 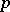 -adic integers. A quasi-cyclic group is the union of an ascending chain of cyclic groups
-adic integers. A quasi-cyclic group is the union of an ascending chain of cyclic groups 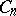 of orders
of orders 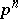 ,
, 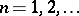 ; more precisely, it is the inductive limit
; more precisely, it is the inductive limit
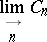 |
with respect to the inductive system 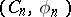 . This group can be defined in terms of generators and relations as the group with countable system of generators
. This group can be defined in terms of generators and relations as the group with countable system of generators 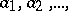 and relations
and relations
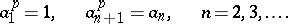 |
Quasi-cyclic groups are the only infinite Abelian (and also the only locally-finite infinite) groups all subgroups of which are finite. The question of the existence of infinite non-Abelian groups with this property is still unsolved (1978) and constitutes one of the problems of O.Yu. Shmidt.
Quasi-cyclic groups are divisible Abelian groups (cf. Divisible group), and each divisible Abelian group is the direct sum of a set of groups that are isomorphic to the additive group of rational numbers and to quasi-cyclic groups for certain prime numbers 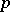 . Groups of type
. Groups of type 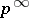 are maximal
are maximal 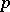 -subgroups of the multiplicative group of complex numbers, and also maximal
-subgroups of the multiplicative group of complex numbers, and also maximal 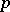 -subgroups of the additive group of rational numbers modulo 1. The ring of endomorphisms of a group of type
-subgroups of the additive group of rational numbers modulo 1. The ring of endomorphisms of a group of type 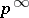 is isomorphic to the ring of
is isomorphic to the ring of 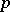 -adic integers. A quasi-cyclic group coincides with its Frattini subgroup.
-adic integers. A quasi-cyclic group coincides with its Frattini subgroup.
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
A quasi-cyclic group is better known as a Prüfer group in the West.
Quasi-cyclic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-cyclic_group&oldid=14132