Quantum sphere
A 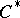 -algebra
-algebra  generated by two elements
generated by two elements 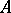 and
and 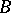 satisfying [a1]
satisfying [a1]
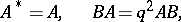 |
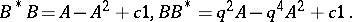 |
Here,  is a deformation parameter and
is a deformation parameter and 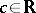 is another parameter labeling the family of quantum spheres. Each quantum sphere is a quantum homogeneous space in the sense that there exists a right co-action
is another parameter labeling the family of quantum spheres. Each quantum sphere is a quantum homogeneous space in the sense that there exists a right co-action
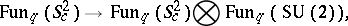 |
where 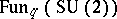 stands for the quantum group
stands for the quantum group 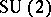 [a7] (cf. also Quantum groups) considered as a deformation of the Poisson algebra
[a7] (cf. also Quantum groups) considered as a deformation of the Poisson algebra 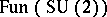 . The one-parameter family of quantum spheres is in correspondence with the family of
. The one-parameter family of quantum spheres is in correspondence with the family of 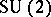 -covariant Poisson structures on
-covariant Poisson structures on 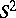 , which is known to be one-parametric too ([a2], Appendix). The deformation of the Poisson structure
, which is known to be one-parametric too ([a2], Appendix). The deformation of the Poisson structure 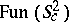 can be introduced in a precisely defined manner [a2]. Also, the structure of representations of
can be introduced in a precisely defined manner [a2]. Also, the structure of representations of 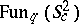 is in correspondence with the structure of symplectic leaves on
is in correspondence with the structure of symplectic leaves on  [a1], [a2]. For
[a1], [a2]. For  , the symplectic leaves are two open discs and the points of a circle separating them. For
, the symplectic leaves are two open discs and the points of a circle separating them. For  , one disc leaf is attached to one one-point leaf and, in fact, this is the Bruhat decomposition of the Poisson homogeneous space
, one disc leaf is attached to one one-point leaf and, in fact, this is the Bruhat decomposition of the Poisson homogeneous space  . For
. For 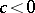 ,
,  is a symplectic manifold.
is a symplectic manifold.
The symplectic spheres 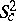 , with
, with 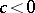 , can be realized as orbits of the dressing transformation of
, can be realized as orbits of the dressing transformation of 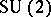 acting on its dual Poisson Lie group. An equivalent realization is given by the right
acting on its dual Poisson Lie group. An equivalent realization is given by the right 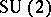 -action on the manifold
-action on the manifold 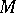 of
of  unimodular positive matrices, which is just the unitary transformation
unimodular positive matrices, which is just the unitary transformation 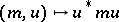 . There exists a quantum analogue as a right co-action
. There exists a quantum analogue as a right co-action  , which is defined formally in the same way as in the Poisson case. If
, which is defined formally in the same way as in the Poisson case. If 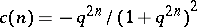 ,
, 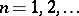 , one can construct, using this structure, the
, one can construct, using this structure, the  -dimensional irreducible representation of the deformed universal enveloping algebra
-dimensional irreducible representation of the deformed universal enveloping algebra 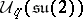 [a3]. Moreover, if
[a3]. Moreover, if 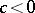 , then the
, then the 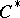 -algebra
-algebra 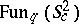 is non-trivial only for
is non-trivial only for 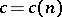 [a1].
[a1].
A few other concepts have been developed for quantum spheres, including a description in terms of a local holomorphic coordinate  and its adjoint
and its adjoint 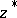 [a3], [a4] and a differential and integral calculus [a4], [a5]. In a precise analogy with the classical case, quantum spherical functions were defined as special basis elements in
[a3], [a4] and a differential and integral calculus [a4], [a5]. In a precise analogy with the classical case, quantum spherical functions were defined as special basis elements in
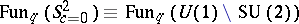 |
and expressed in terms of big  -Jacobi polynomials [a6].
-Jacobi polynomials [a6].
References
| [a1] | P. Podles, "Quantum spheres" Lett. Math. Phys. , 14 (1987) pp. 193–202 |
| [a2] | A.J.L. Sheu, "Quantization of the Poisson  and its Poisson homogeneous space — the and its Poisson homogeneous space — the  -sphere" Comm. Math. Phys. , 135 (1991) pp. 217–232 -sphere" Comm. Math. Phys. , 135 (1991) pp. 217–232 |
| [a3] | P. Šťovíček, "Quantum line bundles on 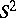 and the method of orbits for and the method of orbits for  " J. Math. Phys. , 34 (1993) pp. 1606–1613 " J. Math. Phys. , 34 (1993) pp. 1606–1613 |
| [a4] | C.S. Chu, P.M. Ho, B. Zumino, "The quantum  -sphere as a complex manifold" Z. Phys. C , 70 (1996) pp. 339–344 -sphere as a complex manifold" Z. Phys. C , 70 (1996) pp. 339–344 |
| [a5] | P. Podles, "Differential calculus on quantum spheres" Lett. Math. Phys. , 18 (1989) pp. 107–119 |
| [a6] | M. Noumi, K. Mimachi, "Quantum  -spheres and big -spheres and big 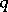 -Jacobi polynomials" Comm. Math. Phys. , 128 (1990) pp. 521–531 -Jacobi polynomials" Comm. Math. Phys. , 128 (1990) pp. 521–531 |
| [a7] | S.L. Woronowicz, "Twisted 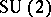 group. An example of a non-commutative differential calculus" Publ. RIMS Univ. Kyoto , 23 (1987) pp. 117–181 group. An example of a non-commutative differential calculus" Publ. RIMS Univ. Kyoto , 23 (1987) pp. 117–181 |
Quantum sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_sphere&oldid=13378