Quantum Grassmannian
A subalgebra  in the algebra
in the algebra  of regular functions on the quantum group
of regular functions on the quantum group  (cf. Quantum groups).
(cf. Quantum groups).  is generated by quantum minors
is generated by quantum minors  , with
, with  and with
and with  the vector co-representation of
the vector co-representation of 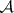 [a1]. The
[a1]. The  -minors satisfy quadratic relations, which turn into the Plücker relations (Young symmetries, cf. also Grassmann manifold) when the deformation parameter
-minors satisfy quadratic relations, which turn into the Plücker relations (Young symmetries, cf. also Grassmann manifold) when the deformation parameter 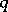 is specialized to
is specialized to 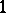 . Since classically the Grassmannian, as a complex submanifold in the projective space
. Since classically the Grassmannian, as a complex submanifold in the projective space  , is the common zero locus of the Plücker relations, one interprets
, is the common zero locus of the Plücker relations, one interprets 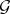 as a quantization of the complex Poisson manifold
as a quantization of the complex Poisson manifold 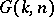 (cf. Symplectic structure). The co-multiplication
(cf. Symplectic structure). The co-multiplication 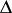 in
in 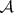 induces a right co-action
induces a right co-action 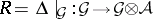 and so
and so 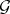 is a quantum homogeneous space.
is a quantum homogeneous space.
A more general construction of (generalized) quantum flag manifolds exists for the group 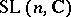 [a1], as well as for other simple complex Lie groups
[a1], as well as for other simple complex Lie groups 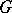 having quantum counterparts [a2]. Another description was given in [a3]. Both approaches [a2], [a3] also allow one to define quantum Schubert varieties.
having quantum counterparts [a2]. Another description was given in [a3]. Both approaches [a2], [a3] also allow one to define quantum Schubert varieties.
Since 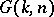 is compact, the only holomorphic functions defined globally on it are the constants. But one can work instead with holomorphic coordinates
is compact, the only holomorphic functions defined globally on it are the constants. But one can work instead with holomorphic coordinates 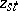 ,
, 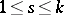 ,
,  , on the big cell
, on the big cell 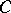 , the unique Schubert cell of top dimension. The standard choice of coordinates is given via the Gauss decomposition of
, the unique Schubert cell of top dimension. The standard choice of coordinates is given via the Gauss decomposition of 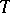 . For the algebra
. For the algebra  this means in fact a localization by allowing the
this means in fact a localization by allowing the  -minor
-minor  to be invertible. The generators
to be invertible. The generators 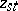 of the quantum big cell
of the quantum big cell 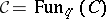 satisfy the relations [a4]
satisfy the relations [a4]
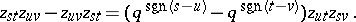 |
The symplectic manifold 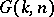 can be realized as an orbit of the dressing transformation of
can be realized as an orbit of the dressing transformation of  acting on its dual Poisson Lie group. The transformation can be also viewed as the right
acting on its dual Poisson Lie group. The transformation can be also viewed as the right 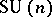 -action on the manifold
-action on the manifold 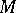 of
of  unimodular positive matrices:
unimodular positive matrices: 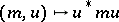 . The orbits are determined by sets of eigenvalues and
. The orbits are determined by sets of eigenvalues and 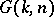 corresponds to a two-point set
corresponds to a two-point set 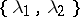 with multiplicities
with multiplicities 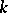 and
and 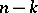 , respectively. There exists a quantum analogue as a right co-action
, respectively. There exists a quantum analogue as a right co-action
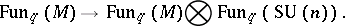 |
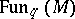 is endowed with a
is endowed with a  -involution and, correspondingly, one can turn
-involution and, correspondingly, one can turn  into a
into a  -algebra by determining the commutation relations between
-algebra by determining the commutation relations between 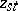 and
and 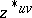 in dependence on the parameters
in dependence on the parameters  and
and 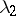 [a4].
[a4].
Similarly as for quantum spheres (cf. Quantum sphere), other types of quantum Grassmannians have been defined, distinguished by possessing classical points, i.e., one-dimensional representations 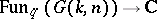 [a5].
[a5].
References
| [a1] | E. Taft, J. Towber, "Quantum deformations of flag schemes and Grassmann schemes I. A 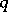 -deformation for the shape algebra -deformation for the shape algebra 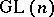 " J. Algebra , 142 (1991) pp. 1–36 " J. Algebra , 142 (1991) pp. 1–36 |
| [a2] | Ya.S. Soibelman, "On the quantum flag manifold" Funct. Anal. Appl. , 26 (1992) pp. 225–227 |
| [a3] | V. Lakshmibai, N. Reshetikhin, "Quantum deformations of flag and Schubert schemes" C.R. Acad. Sci. Paris , 313 (1991) pp. 121–126 |
| [a4] | P. Šťovíček, "Quantum Grassmann manifolds" Comm. Math. Phys. , 158 (1993) pp. 135–153 |
| [a5] | M. Nuomi, M.S. Dijkhuizen, T. Sugitani, "Multivariable Askey–Wilson polynomials and quantum complex Grassmannians" M.E.H. Insmail (ed.) et al. (ed.) , Special Functions, 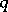 -Series and Related Topics , Fields Inst. Commun. , 14 , Amer. Math. Soc. (1997) pp. 167–177 -Series and Related Topics , Fields Inst. Commun. , 14 , Amer. Math. Soc. (1997) pp. 167–177 |
Quantum Grassmannian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_Grassmannian&oldid=15744