Quantifier
The general name for a logical operation that constructs from a predicate  a statement characterizing the domain of validity of
a statement characterizing the domain of validity of  . In mathematical logic, the most widely used quantifiers are the universal quantifier
. In mathematical logic, the most widely used quantifiers are the universal quantifier  and the existential quantifier
and the existential quantifier  . The statement
. The statement  means that the domain of validity of
means that the domain of validity of  is the same as the domain of values of the variable
is the same as the domain of values of the variable  . The statement
. The statement  means that the domain of validity of
means that the domain of validity of  is non-empty. If one is interested in the behaviour of the predicate
is non-empty. If one is interested in the behaviour of the predicate  not on the whole domain of values of
not on the whole domain of values of  , but only on the part singled out by a predicate
, but only on the part singled out by a predicate 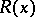 , then one often uses the restricted quantifiers
, then one often uses the restricted quantifiers  and
and 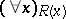 . In this case, the statement
. In this case, the statement 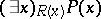 means the same as
means the same as  , while
, while 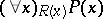 has the same meaning as
has the same meaning as 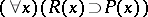 , where
, where 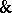 is the conjunction sign and
is the conjunction sign and  is the implication sign.
is the implication sign.
Comments
The subject of quantifiers nowadays is far more involved than suggested above, since there are many more quantifiers (e.g. game quantifiers, probability quantifiers) than just the two (or four) discussed above.
More generally, the model-theoretic interpretation of an arbitrary "quantifier"  (with the same syntactic behaviour as
(with the same syntactic behaviour as  and
and  ) can (according to A. Mostowski) be given by a mapping associating with each model
) can (according to A. Mostowski) be given by a mapping associating with each model 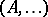 a class
a class 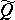 of subsets of
of subsets of  . Then one stipulates as a truth-definition for
. Then one stipulates as a truth-definition for  that, e.g., a sentence
that, e.g., a sentence  holds in
holds in 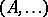 if and only if the set
if and only if the set 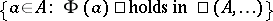 is in
is in  . Thus, with the existential quantifier
. Thus, with the existential quantifier  is associated the class of non-empty subsets of
is associated the class of non-empty subsets of  and with the universal quantifier
and with the universal quantifier  is associated the class
is associated the class  . However, there are many more possible quantifiers, e.g. given by
. However, there are many more possible quantifiers, e.g. given by  ,
, 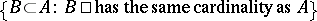 (the Chang quantifier),
(the Chang quantifier),  , etc. This set-up can be generalized to "quantifiers" binding more than one variable occurring in more than one formula (example: the equi-cardinality quantifier
, etc. This set-up can be generalized to "quantifiers" binding more than one variable occurring in more than one formula (example: the equi-cardinality quantifier 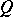 binding two variables
binding two variables  and
and 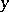 in two formulas
in two formulas  and
and 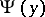 , yielding the formula
, yielding the formula  , which is interpreted by
, which is interpreted by  ). Even more general is the Lindström quantifier. And each quantifier has its own logic.
). Even more general is the Lindström quantifier. And each quantifier has its own logic.
References
| [a1] | J. Barwise (ed.) S. Feferman (ed.) , Model-theoretic logics , Springer (1985) |
Quantifier. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantifier&oldid=14021