Qualitative theory of differential equations in Banach spaces
A branch of functional analysis in which one studies the behaviour on the real axis 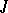 or on the positive (or negative) semi-axis
or on the positive (or negative) semi-axis 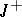 (or
(or 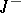 ) of the solution of the evolution equation in a Banach space. Consider the equations
) of the solution of the evolution equation in a Banach space. Consider the equations
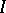 .
. 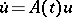 ;
;
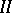 .
. 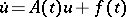 ;
;
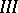 .
. 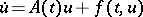 , where
, where 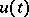 is the required function and
is the required function and 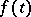 the given function with values in a complex Banach space
the given function with values in a complex Banach space 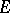 ;
; 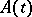 is a linear operator and
is a linear operator and 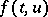 is a non-linear operator on
is a non-linear operator on 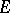 . By the derivative
. By the derivative 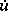 one means the limit in the norm of
one means the limit in the norm of 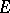 of
of 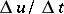 as
as 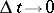 .
.
Uniform stability holds for the equation 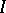 if there exists a constant
if there exists a constant 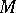 such that for any solution
such that for any solution 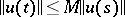 ,
, 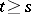 , and exponential stability if for any solution
, and exponential stability if for any solution 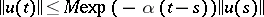 for some
for some 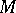 and
and 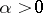 .
.
For equation 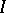 with a constant bounded operator
with a constant bounded operator 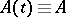 , the solution of the Cauchy problem (
, the solution of the Cauchy problem (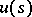 given) has the form
given) has the form 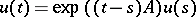 . The estimate
. The estimate 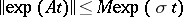 holds, where
holds, where 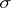 is a number greater than the real parts of all points of the spectrum of
is a number greater than the real parts of all points of the spectrum of 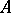 . Thus, for exponential stability it is necessary and sufficient that the spectrum of
. Thus, for exponential stability it is necessary and sufficient that the spectrum of 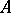 lies in the interior of the left half-plane. In a Hilbert space this holds if and only if there exists a positive-definite form
lies in the interior of the left half-plane. In a Hilbert space this holds if and only if there exists a positive-definite form 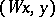 for which
for which 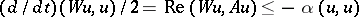 for every solution of the equation (Lyapunov's theorem). If the spectrum of
for every solution of the equation (Lyapunov's theorem). If the spectrum of 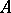 is distributed on both sides of the imaginary axis and does not intersect it, then
is distributed on both sides of the imaginary axis and does not intersect it, then 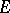 can be decomposed into a direct sum of subspaces
can be decomposed into a direct sum of subspaces 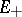 and
and 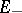 which are invariant with respect to
which are invariant with respect to 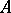 , and all the solutions are exponentially increasing (decreasing) in
, and all the solutions are exponentially increasing (decreasing) in 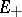 (
(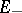 ) as
) as 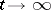 . In this case, exponential dichotomy holds for the equation.
. In this case, exponential dichotomy holds for the equation.
If 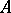 is closed, unbounded and has a dense domain in
is closed, unbounded and has a dense domain in 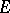 , then the Cauchy problem with
, then the Cauchy problem with 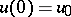 is not, in general, well-posed. The existence and properties of the solutions are not determined merely by the distribution of the spectrum of
is not, in general, well-posed. The existence and properties of the solutions are not determined merely by the distribution of the spectrum of 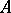 ; the behaviour of its resolvent
; the behaviour of its resolvent 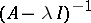 must also be specified. Commonly used conditions ensuring the uniform well-posedness of the Cauchy problem on
must also be specified. Commonly used conditions ensuring the uniform well-posedness of the Cauchy problem on 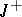 are provided by the inequalities
are provided by the inequalities
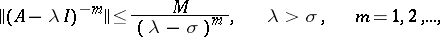 |
a sufficient condition for their fulfillment being the Hille–Yosida condition
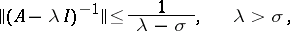 |
or the inequality
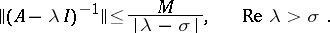 |
When these conditions hold, the solution of the Cauchy problem has the form 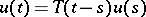 , where
, where 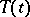 is a strongly-continuous semi-group of operators for
is a strongly-continuous semi-group of operators for 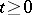 and
and 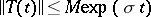 . For uniform (or exponential) stability it suffices that
. For uniform (or exponential) stability it suffices that 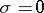 (respectively,
(respectively, 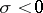 ). If
). If 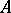 generates a strongly-continuous semi-group on a Hilbert space, then the sufficiency part of Lyapunov's theorem holds for it, while if it generates a group, then the necessity part holds as well. In a Hilbert space exponential stability is equivalent to
generates a strongly-continuous semi-group on a Hilbert space, then the sufficiency part of Lyapunov's theorem holds for it, while if it generates a group, then the necessity part holds as well. In a Hilbert space exponential stability is equivalent to 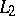 -stability, the property that for all solutions
-stability, the property that for all solutions 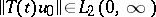 .
.
Important for applications is the property of almost-periodicity of the solution 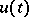 or weak almost-periodicity (that is, almost periodicity of the scalar functions
or weak almost-periodicity (that is, almost periodicity of the scalar functions 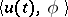 for all
for all 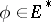 ). If all values of an almost-periodic solution lie in a compact set, then the solution is compact. Compactness and weak almost-periodicity imply almost-periodicity. For the equation
). If all values of an almost-periodic solution lie in a compact set, then the solution is compact. Compactness and weak almost-periodicity imply almost-periodicity. For the equation 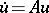 , the question of almost-periodicity of the solution is related to the structure of the intersection of the spectrum of
, the question of almost-periodicity of the solution is related to the structure of the intersection of the spectrum of 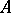 with the imaginary axis. If
with the imaginary axis. If 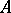 is the generating operator of a bounded strongly-continuous semi-group and the above intersection is countable, then for the almost-periodicity of a bounded solution defined on the whole axis it is necessary and sufficient that the limit
is the generating operator of a bounded strongly-continuous semi-group and the above intersection is countable, then for the almost-periodicity of a bounded solution defined on the whole axis it is necessary and sufficient that the limit 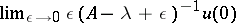 exists at each limit point
exists at each limit point 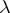 of the spectrum on the imaginary axis. Furthermore, each uniformly-continuous solution is weakly almost-periodic; it is almost-periodic if it is weakly compact, or if
of the spectrum on the imaginary axis. Furthermore, each uniformly-continuous solution is weakly almost-periodic; it is almost-periodic if it is weakly compact, or if 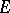 contains no subspaces isomorphic to the space
contains no subspaces isomorphic to the space 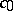 of sequences converging to zero, endowed with the max norm. If
of sequences converging to zero, endowed with the max norm. If 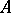 is the generating operator of a strongly-continuous semi-group
is the generating operator of a strongly-continuous semi-group 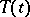 with the property that the functions
with the property that the functions 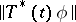 are bounded on
are bounded on 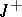 for a set of functionals
for a set of functionals 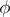 which are dense in
which are dense in 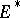 , then compactness of a solution implies almost-periodicity.
, then compactness of a solution implies almost-periodicity.
For equation 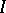 with a bounded operator
with a bounded operator 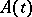 that is continuous in
that is continuous in 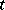 , the solutions of the Cauchy problem are defined on the whole axis and, by means of the evolution operator
, the solutions of the Cauchy problem are defined on the whole axis and, by means of the evolution operator 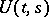 , can be written in the form
, can be written in the form 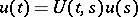 . The property of uniform stability is equivalent to the requirement that
. The property of uniform stability is equivalent to the requirement that 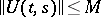 ; the property of exponential stability is equivalent to
; the property of exponential stability is equivalent to 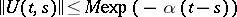 . If
. If 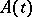 is bounded in integral norm, that is,
is bounded in integral norm, that is, 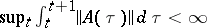 , then the general index
, then the general index
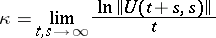 |
is finite. If 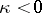 , one has exponential stability. For equations with a constant or periodic operator, the formula
, one has exponential stability. For equations with a constant or periodic operator, the formula 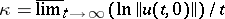 holds. It does not hold in the general case. The general index is not altered if
holds. It does not hold in the general case. The general index is not altered if 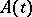 is perturbed by adding a term
is perturbed by adding a term 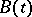 for which
for which 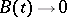 as
as 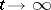 , or for which the integral
, or for which the integral 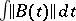 converges at infinity. The size of the general index depends on the behaviour of
converges at infinity. The size of the general index depends on the behaviour of 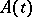 at infinity. If the limit
at infinity. If the limit 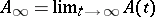 exists and the spectrum of
exists and the spectrum of  lies in the interior of the left half-plane, then
lies in the interior of the left half-plane, then 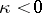 . If the operators
. If the operators 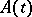 ,
, 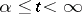 , form a compact set in the space of bounded operators, if the spectra of all limit operators belong to a half-plane
, form a compact set in the space of bounded operators, if the spectra of all limit operators belong to a half-plane 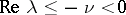 and if the operator function
and if the operator function 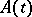 has small oscillation, for example, it has the form
has small oscillation, for example, it has the form 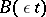 for sufficiently small
for sufficiently small  , or if, for sufficiently large
, or if, for sufficiently large 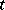 , it satisfies the Lipschitz condition
, it satisfies the Lipschitz condition 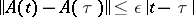 with
with  sufficiently small, then
sufficiently small, then 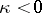 . In a Hilbert space the condition
. In a Hilbert space the condition 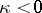 is equivalent to the existence of a Hermitian form
is equivalent to the existence of a Hermitian form 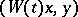 such that
such that 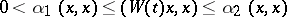 and
and 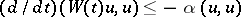 for every solution
for every solution 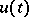 .
.
If 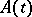 is periodic with period
is periodic with period 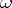 , i.e. if
, i.e. if 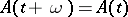 , then
, then 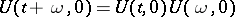 . The operator
. The operator 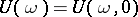 is called the monodromy operator of equation
is called the monodromy operator of equation 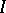 . Its spectral radius
. Its spectral radius 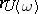 is related to the general index by the formula
is related to the general index by the formula 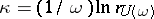 . The equation has a periodic solution if and only if 1 is an eigen value of
. The equation has a periodic solution if and only if 1 is an eigen value of 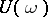 . If the operator
. If the operator 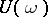 has a logarithm, then the Floquet representation
has a logarithm, then the Floquet representation 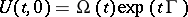 holds, where
holds, where 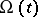 is periodic with period
is periodic with period 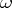 and
and 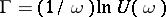 . In particular, the Floquet representation holds if the spectrum of
. In particular, the Floquet representation holds if the spectrum of 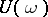 does not surround the origin; and for this it suffices that
does not surround the origin; and for this it suffices that 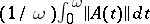 be less than a certain constant, which depends on the geometry of the sphere in
be less than a certain constant, which depends on the geometry of the sphere in 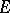 and which is not less than
and which is not less than 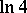 . For Hilbert space this constant is
. For Hilbert space this constant is 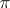 . The Floquet representation reduces the question of the behaviour of the solution of the equation to the same question for the equation
. The Floquet representation reduces the question of the behaviour of the solution of the equation to the same question for the equation 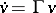 with a constant operator
with a constant operator 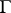 .
.
Exponential dichotomy holds for equation 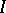 if for some
if for some  the space decomposes into a direct sum of subspaces
the space decomposes into a direct sum of subspaces 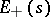 and
and 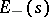 such that
such that
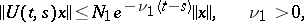 |
when 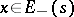 ,
, 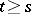 , and
, and
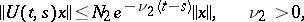 |
when 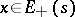 ,
, 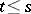 . It is supposed here that the subsequences
. It is supposed here that the subsequences 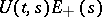 and
and  are, in a certain sense, not close to each other. If the general index is finite, this latter requirement holds automatically. For an equation with a periodic
are, in a certain sense, not close to each other. If the general index is finite, this latter requirement holds automatically. For an equation with a periodic 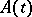 , a necessary and sufficient condition for exponential dichotomy to hold is that the spectrum of the monodromy operator be distributed outside and inside the unit disc without intersecting the unit circle.
, a necessary and sufficient condition for exponential dichotomy to hold is that the spectrum of the monodromy operator be distributed outside and inside the unit disc without intersecting the unit circle.
For equation 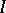 with an unbounded operator
with an unbounded operator 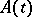 whose domain does not depend on
whose domain does not depend on 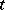 and which satisfies the well-posedness conditions for the Cauchy problem (see above) for every
and which satisfies the well-posedness conditions for the Cauchy problem (see above) for every 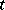 , the existence of an evolution operator
, the existence of an evolution operator 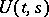 , defined and strongly continuous in
, defined and strongly continuous in  and
and  for
for 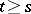 , has been proved, under supplementary smoothness conditions. This enables one to carry over to this case a number of the ideas and results described above. However, some difficulties are encountered. E.g., the Floquet representation can be obtained only in a Hilbert space when
, has been proved, under supplementary smoothness conditions. This enables one to carry over to this case a number of the ideas and results described above. However, some difficulties are encountered. E.g., the Floquet representation can be obtained only in a Hilbert space when 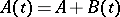 , where
, where 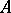 is a negative-definite self-adjoint operator and
is a negative-definite self-adjoint operator and 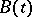 is a bounded periodic operator satisfying certain extra conditions.
is a bounded periodic operator satisfying certain extra conditions.
Suppose that 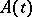 is periodic and that the Cauchy problem for equation
is periodic and that the Cauchy problem for equation 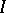 is uniformly well-posed. If the intersection of the spectrum of the monodromy operator
is uniformly well-posed. If the intersection of the spectrum of the monodromy operator 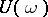 with the unit circle is countable, then each bounded uniformly-continuous solution on
with the unit circle is countable, then each bounded uniformly-continuous solution on 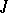 is weakly almost-periodic. It is almost-periodic in the case of weak compactness or if
is weakly almost-periodic. It is almost-periodic in the case of weak compactness or if 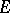 does not contain
does not contain 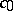 . A reflexive space
. A reflexive space 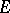 admits a direct sum decomposition
admits a direct sum decomposition 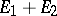 such that
such that 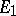 and
and 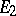 are invariant with respect to
are invariant with respect to 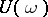 and all the solutions starting in
and all the solutions starting in 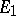 are almost-periodic, while those starting in
are almost-periodic, while those starting in 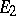 are in a certain sense decreasing: For
are in a certain sense decreasing: For 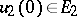 ,
,  ,
,
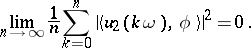 |
For the solution of the non-homogeneous equation  , the following formula holds:
, the following formula holds:
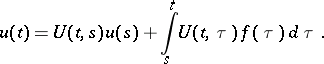 |
For an equation with a bounded operator, this equation is equivalent to the differential equation. In the case of an unbounded operator, this is generally not so, but then this equation is taken as the definition of the (generalized) solution. The fundamental problem for equation 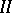 is to investigate the properties of the solutions under prescribed properties of the right-hand side. These properties are usually described in terms of the function
is to investigate the properties of the solutions under prescribed properties of the right-hand side. These properties are usually described in terms of the function 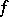 belonging to some Banach space of functions on
belonging to some Banach space of functions on 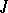 or
or 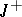 with values in
with values in 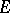 . If corresponding to each bounded continuous function
. If corresponding to each bounded continuous function 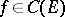 there is at least one bounded solution, then the operator
there is at least one bounded solution, then the operator 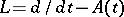 is called weakly regular. If corresponding to each
is called weakly regular. If corresponding to each 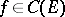 there is a unique solution
there is a unique solution 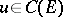 , then
, then 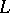 is called regular. For bounded constant
is called regular. For bounded constant 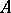 , weak regularity implies regularity. This assertion is no longer true for unbounded
, weak regularity implies regularity. This assertion is no longer true for unbounded 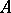 or for bounded periodic
or for bounded periodic 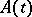 , even in a Hilbert space. If the general index of the equation
, even in a Hilbert space. If the general index of the equation 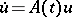 is finite, then exponential dichotomy for this equation is equivalent to regularity of
is finite, then exponential dichotomy for this equation is equivalent to regularity of 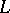 on
on 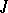 . For exponential dichotomy to hold on
. For exponential dichotomy to hold on 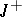 it is necessary and sufficient that
it is necessary and sufficient that 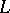 be weakly regular on
be weakly regular on 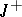 and that the set of those initial values
and that the set of those initial values 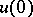 to which the bounded solutions of equation
to which the bounded solutions of equation 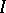 correspond be a complemented subspace of
correspond be a complemented subspace of 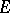 . If for all solutions of
. If for all solutions of 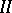 the inequality
the inequality
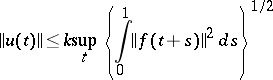 |
holds, and if for the solution of the formal adjoint equation 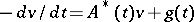 the inequality
the inequality 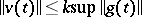 holds, then the operators
holds, then the operators 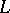 and
and 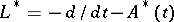 are regular. It is not known (1990) whether regularity is preserved on replacing the right-hand side of the first inequality by
are regular. It is not known (1990) whether regularity is preserved on replacing the right-hand side of the first inequality by 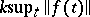 . For the regularity of
. For the regularity of 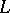 and
and 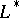 both, a priori estimates are necessary.
both, a priori estimates are necessary.
If 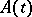 is periodic, then a necessary and sufficient condition for the existence of periodic solutions for each periodic
is periodic, then a necessary and sufficient condition for the existence of periodic solutions for each periodic 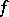 is that the mapping
is that the mapping 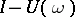 be surjective, while for such a solution to be unique, it is necessary and sufficient that the operator
be surjective, while for such a solution to be unique, it is necessary and sufficient that the operator 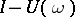 be invertible.
be invertible.
The verification of regularity under known conditions can be reduced to the verification of the regularity of operators with constant coefficients. In the case when  is strongly oscillating (for example
is strongly oscillating (for example 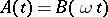 with
with 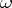 large), under the assumption that the mean
large), under the assumption that the mean
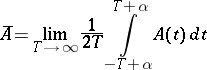 |
exists uniformly with respect to 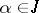 , the operator
, the operator 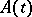 is regular if and only if the operator
is regular if and only if the operator 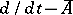 is regular.
is regular.
For almost-periodic solutions the specifics of an infinite-dimensional space are already encountered in a generalization of the well-known Bohl–Bohr theorem on the almost-periodicity of a bounded integral of an almost-periodic function, that is, on the almost-periodicity of a solution of the simplest differential equation 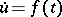 . If the indefinite integral of an almost-periodic function with values in
. If the indefinite integral of an almost-periodic function with values in 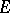 is bounded in
is bounded in 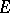 and
and 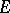 does not contain
does not contain 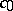 , then the function is almost-periodic. The Bohl–Bohr theorem fails in
, then the function is almost-periodic. The Bohl–Bohr theorem fails in 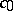 . If
. If 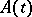 is periodic,
is periodic, 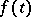 is almost-periodic and the intersection of the spectrum of the monodromy operator
is almost-periodic and the intersection of the spectrum of the monodromy operator 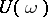 with the unit circle is countable, then the same conclusions on the almost-periodicity of solutions stated earlier for the homogeneous equation hold for this case. If
with the unit circle is countable, then the same conclusions on the almost-periodicity of solutions stated earlier for the homogeneous equation hold for this case. If 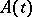 is almost-periodic (as a function with values in the space of bounded operators on
is almost-periodic (as a function with values in the space of bounded operators on 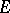 ), then in order that for each almost-periodic function
), then in order that for each almost-periodic function 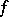 there exists a unique almost-periodic solution, it is necessary and sufficient that
there exists a unique almost-periodic solution, it is necessary and sufficient that 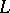 be regular. If equation
be regular. If equation 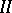 has a (weakly) compact solution for
has a (weakly) compact solution for 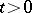 , and the non-trivial (weakly) compact solutions of the homogeneous equation
, and the non-trivial (weakly) compact solutions of the homogeneous equation 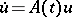 have the property that
have the property that 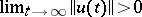 , then equation
, then equation 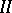 has a (weakly) almost-periodic solution.
has a (weakly) almost-periodic solution.
In the qualitative study of a non-linear equation 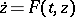 , it is usually supposed in advance that conditions hold which ensure that solutions exist on
, it is usually supposed in advance that conditions hold which ensure that solutions exist on 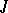 or on
or on  ; this imposes an essential constraint on the form of non-linearity of
; this imposes an essential constraint on the form of non-linearity of 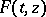 . A solution
. A solution 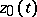 on
on 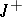 is said to be uniformly stable if there exists for each
is said to be uniformly stable if there exists for each 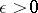 a
a 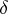 such that for every other solution
such that for every other solution 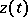 the inequality
the inequality 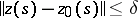 ,
, 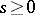 , implies that
, implies that  is defined for
is defined for 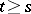 and that
and that 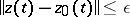 . A solution is called asymptotically stable if it is uniformly stable and if for some
. A solution is called asymptotically stable if it is uniformly stable and if for some 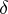 the inequality
the inequality 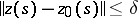 implies that
implies that 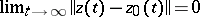 . If one makes the substitution
. If one makes the substitution 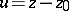 in the equation, then after linearization (if this is possible) it takes the form
in the equation, then after linearization (if this is possible) it takes the form 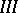 , where
, where 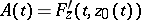 , and the non-linearity has the property that
, and the non-linearity has the property that 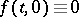 . Thus the problem of uniform (asymptotic) stability of the solution
. Thus the problem of uniform (asymptotic) stability of the solution  reduces to that of the uniform (or asymptotic) stability of the zero solution of
reduces to that of the uniform (or asymptotic) stability of the zero solution of 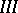 . In this connection, the equation
. In this connection, the equation 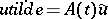 is called the linearization equation (or variational equation) of the original equation with respect to the solution
is called the linearization equation (or variational equation) of the original equation with respect to the solution 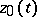 .
.
If the non-linear part 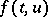 is sufficiently small, then the properties of the solutions are determined by those of the linearized equation. If the general index of the linearized equation is negative and the inequality
is sufficiently small, then the properties of the solutions are determined by those of the linearized equation. If the general index of the linearized equation is negative and the inequality 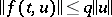 ,
, 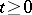 ,
, 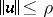 , holds, then for sufficiently small
, holds, then for sufficiently small 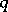 the zero solution of
the zero solution of 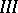 is asymptotically stable. If
is asymptotically stable. If 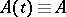 and the spectrum of
and the spectrum of 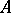 does not intersect the imaginary axis and has a point in the right half-plane, then for sufficiently small
does not intersect the imaginary axis and has a point in the right half-plane, then for sufficiently small 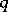 the zero solution is unstable. If the inequality
the zero solution is unstable. If the inequality
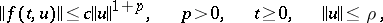 |
holds, then the requirement that there be no points of the spectrum on the imaginary axis can be deleted.
If exponential dichotomy holds on 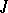 for the linearized equation, then for every
for the linearized equation, then for every 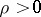 there exist
there exist 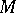 and
and  depending on
depending on 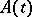 and
and 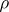 such that the inequalities
such that the inequalities
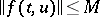 |
and
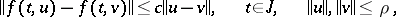 |
imply the existence, in some neighbourhood of the origin, of two manifolds 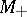 and
and 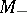 , intersecting at the single point
, intersecting at the single point 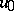 , such that the solution
, such that the solution  starting at
starting at 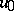 is bounded on the entire axis and
is bounded on the entire axis and 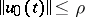 ; solutions starting on
; solutions starting on 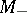 (
(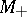 ) approach
) approach  exponentially as
exponentially as 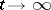 (
(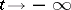 ) and move away from it as
) and move away from it as 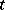 goes to infinity in the opposite direction. Furthermore,
goes to infinity in the opposite direction. Furthermore, 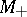 (
(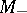 ) is homeomorphic to the neighbourhood of the space
) is homeomorphic to the neighbourhood of the space 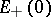 (
(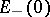 ) involved in the definition of exponential dichotomy. If under the above conditions
) involved in the definition of exponential dichotomy. If under the above conditions 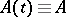 and
and 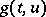 is almost-periodic in
is almost-periodic in 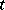 for each
for each  with
with 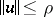 , then the solution
, then the solution  is almost-periodic.
is almost-periodic.
Suppose that the autonomous equation 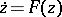 has an
has an 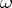 -periodic solution
-periodic solution 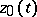 ; then the linearized equation
; then the linearized equation 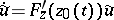 has a single periodic solution
has a single periodic solution 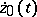 and, consequently, its monodromy operator
and, consequently, its monodromy operator 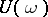 has 1 as eigen value. If this eigen value is simple and the remaining spectrum of
has 1 as eigen value. If this eigen value is simple and the remaining spectrum of 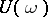 lies in the interior of the unit disc and does not surround the origin, then there exist numbers
lies in the interior of the unit disc and does not surround the origin, then there exist numbers 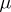 ,
, 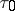 and
and 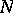 such that
such that 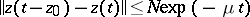 for all other solutions of the original equation. This property is called asymptotic orbital stability of the periodic solution. Studies have also been made of other stable invariant manifolds for non-linear equations.
for all other solutions of the original equation. This property is called asymptotic orbital stability of the periodic solution. Studies have also been made of other stable invariant manifolds for non-linear equations.
Equations of type 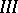 with an unbounded operator
with an unbounded operator 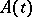 correspond in applications to quasi-linear equations of parabolic or hyperbolic type. A theory of "properly" non-linear equations of a specific type has been developed. Thus, if
correspond in applications to quasi-linear equations of parabolic or hyperbolic type. A theory of "properly" non-linear equations of a specific type has been developed. Thus, if 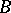 is a continuous everywhere-defined dissipative operator, then the Cauchy problem
is a continuous everywhere-defined dissipative operator, then the Cauchy problem 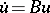 ,
,  , is uniquely solvable on the semi-axis
, is uniquely solvable on the semi-axis 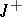 for any
for any 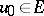 . The definition of a dissipative operator carries over in a natural fashion to the case of a many-valued operator; for such operators one considers a differential inclusion
. The definition of a dissipative operator carries over in a natural fashion to the case of a many-valued operator; for such operators one considers a differential inclusion 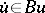 rather than a differential equation. If on a reflexive space
rather than a differential equation. If on a reflexive space 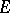 , the operator
, the operator 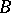 is closed and dissipative and if the values of
is closed and dissipative and if the values of 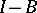 cover the entire space
cover the entire space 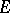 , then the Cauchy problem is uniquely solvable on
, then the Cauchy problem is uniquely solvable on 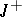 for each
for each 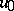 in the domain of
in the domain of 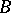 . There are many variants of the latter statement. The solution is given by the formula
. There are many variants of the latter statement. The solution is given by the formula 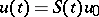 , where
, where 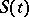 is a semi-group of non-linear operators,
is a semi-group of non-linear operators,  ,
, 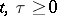 . For equations with dissipative operators there are also existence theorems for periodic and almost-periodic solutions.
. For equations with dissipative operators there are also existence theorems for periodic and almost-periodic solutions.
References
| [1] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [2] | H.H. Schaefer, "Linear differential equations and function spaces" , Acad. Press (1966) |
| [3] | K. Yosida, "Functional analysis" , Springer (1968) |
| [4] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
| [5] | V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian) |
| [6] | A.G. Baskakov, "On the spectral analysis of isometric representations of locally compact Abelian groups" Trudy Mat. Fak. Vorozhen. Inst. , 10 (1973) pp. 96–101 (In Russian) |
| [7] | V.V. Zhikov, "Some admissibility and dichotomy questions. The averaging principle" Math. USSR Izv. , 10 (1976) pp. 1307–1332 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 6 (1976) pp. 1380–1408 |
| [8] | V.V. Zhikov, B.M. Levitan, "Favard theory" Russian Math. Surveys , 32 : 2 (1977) pp. 129–180 Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 123–171 |
| [9] | A.I. Miloslavskii, "Floquet theory for parabolic equations" Funct. Anal. Appl. , 10 : 2 (1976) pp. 151–153 Funktsional. Anal. i Prilozhen. , 10 : 2 (1976) pp. 80–81 |
| [10] | V.M. Tyurin, "Functional analysis" , 1 , Ul'yanovsk (1973) (In Russian) |
| [11] | B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian) |
Comments
For a somewhat different approach to the qualitative theory of abstract differential equations see [a1], [a2].
References
| [a1] | J.K. Hale, "Asymptotic behavior of dissipative systems" , Amer. Math. Soc. (1988) |
| [a2] | J.K. Hale, L.T. Magalhes, W.M. Oliva, "An introduction to infinite dimensional dynamical systems" , Springer (1984) |
Qualitative theory of differential equations in Banach spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Qualitative_theory_of_differential_equations_in_Banach_spaces&oldid=17686