Qualitative theory of differential equations
The mathematical discipline studying the properties of solutions of ordinary differential equations without finding the solutions themselves.
The foundations of the qualitative theory of differential equations were laid at the end of the 19th century by H. Poincaré (see , [2]) and A.M. Lyapunov (see [3], [4]). Poincaré made extensive use of geometric methods, regarding the solutions of systems of differential equations as curves in an appropriate space. On this basis he created a general theory of the behaviour of solutions of second-order differential equations and solved a number of fundamental problems on the dependence of solutions on parameters (see below). Lyapunov studied the behaviour of solutions in a neighbourhood of an equilibrium position. He founded the modern theory of stability of motion (see Stability theory).
The geometric approach of Poincaré was developed in the 1920s by George Birkhoff, who discovered many important facts in the qualitative theory of higher-dimensional systems of differential equations (see [5], [6]).
Linear systems.
Consider the system of differential equations
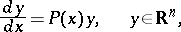 | (1) |
where 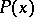 is a square
is a square 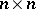 matrix. It is assumed that
matrix. It is assumed that 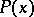 is bounded. (In the unbounded case there have been only a few highly specialized studies.) In the qualitative theory of differential equations one studies the asymptotic behaviour of the solutions of (1) as
is bounded. (In the unbounded case there have been only a few highly specialized studies.) In the qualitative theory of differential equations one studies the asymptotic behaviour of the solutions of (1) as 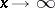 .
.
The characteristic index of a solution 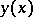 is the quantity
is the quantity
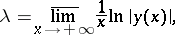 |
characterizing the growth of the solutions as compared to the exponential function (cf. also Lyapunov characteristic exponent). Every non-zero solution of (1) has a finite characteristic index. The characteristic indices of non-zero solutions are also called the characteristic indices of the system. A linear system cannot have more than  distinct characteristic indices. The characteristic indices of a system are not altered by a linear change of variables
distinct characteristic indices. The characteristic indices of a system are not altered by a linear change of variables
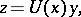 | (2) |
provided that the matrices 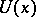 ,
, 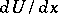 and
and 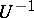 are bounded. Such transformations are called Lyapunov transformations.
are bounded. Such transformations are called Lyapunov transformations.
If 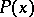 is a constant matrix, the characteristic indices of (1) are the real parts of the eigen values of
is a constant matrix, the characteristic indices of (1) are the real parts of the eigen values of 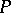 .
.
A linear system is called reducible if there exists a Lyapunov transformation (2) which reduces the system to the form (1) with a constant matrix 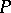 (see [7], [8]).
(see [7], [8]).
If 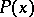 has period
has period 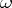 , a fundamental matrix
, a fundamental matrix 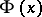 (that is, a matrix consisting of linearly independent solutions) can, according to Floquet's theorem (see [9]), be expressed in the following form:
(that is, a matrix consisting of linearly independent solutions) can, according to Floquet's theorem (see [9]), be expressed in the following form:
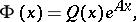 | (3) |
where 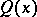 is
is 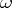 -periodic and
-periodic and 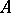 is a constant matrix. Furthermore, if
is a constant matrix. Furthermore, if 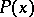 is real, then
is real, then 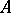 and
and 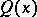 cannot always be chosen real; however, in that case
cannot always be chosen real; however, in that case 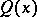 has period
has period 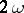 . It follows from (3) that the system (1) with periodic
. It follows from (3) that the system (1) with periodic 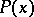 is reducible (Lyapunov's theorem). Formula (3) shows that, for the calculation of the characteristic indices, one merely needs to know
is reducible (Lyapunov's theorem). Formula (3) shows that, for the calculation of the characteristic indices, one merely needs to know 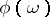 , that is, one needs to calculate the
, that is, one needs to calculate the  different solutions on the interval
different solutions on the interval 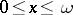 . Linear systems with periodic coefficients have been studied in great detail (see [8], and also Linear system of differential equations with periodic coefficients).
. Linear systems with periodic coefficients have been studied in great detail (see [8], and also Linear system of differential equations with periodic coefficients).
Lyapunov proved (and this is the essence of his first method in stability theory) that a regular system is stable with respect to analytic non-linear perturbations.
One of the interesting problems in the qualitative theory of linear differential equations is that of the oscillatory nature of the solutions of such equations (see Oscillating solution), that is, the problem of the distribution of the zeros of the solutions. For example, if 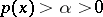 for all
for all  , then every solution of the equation
, then every solution of the equation
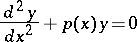 |
has an infinite number of zeros on the interval 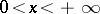 ; moreover, the zeros of two linearly independent solutions alternate (see [10]).
; moreover, the zeros of two linearly independent solutions alternate (see [10]).
Non-linear systems.
General systems of non-linear differential equations are considered in the normal form:
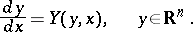 | (4) |
Those studied in greatest detail are autonomous systems (cf. Autonomous system):
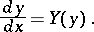 | (5) |
The space of vectors 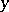 for the system (5) is called phase space. The system (4) can be reduced to the autonomous form (5) by increasing the order by one. An autonomous system of the form (5) defines a dynamical system if all its solutions can be extended to the whole axis
for the system (5) is called phase space. The system (4) can be reduced to the autonomous form (5) by increasing the order by one. An autonomous system of the form (5) defines a dynamical system if all its solutions can be extended to the whole axis  .
.
Let 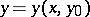 be the solution to (5) with initial data
be the solution to (5) with initial data 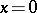 ,
, 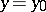 . The curve
. The curve 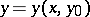 ,
, 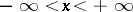 , in the phase space is called a trajectory, while the parts corresponding to
, in the phase space is called a trajectory, while the parts corresponding to 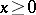 ,
, 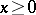 are called semi-trajectories. A special role is played by trajectories which degenerate to a point
are called semi-trajectories. A special role is played by trajectories which degenerate to a point 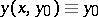 ; this happens if
; this happens if 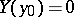 . Such points are called equilibrium states or equilibrium positions. Another important type of trajectory is that of a periodic solution, representing a closed curve in the phase space. A closed trajectory is called a limit cycle if at least one other trajectory converges to it.
. Such points are called equilibrium states or equilibrium positions. Another important type of trajectory is that of a periodic solution, representing a closed curve in the phase space. A closed trajectory is called a limit cycle if at least one other trajectory converges to it.
An important problem in the qualitative theory of non-linear systems is the study of the asymptotic behaviour of all solutions as 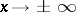 . For autonomous systems of the form (5), this problem reduces to the study of the structure of the limit sets of all the semi-trajectories and the ways the trajectories approach these sets. The limit set of each semi-trajectory is closed and invariant. (A subset of the phase space is called invariant if it consists of complete trajectories.) If a semi-trajectory is bounded, then its limit set is connected.
. For autonomous systems of the form (5), this problem reduces to the study of the structure of the limit sets of all the semi-trajectories and the ways the trajectories approach these sets. The limit set of each semi-trajectory is closed and invariant. (A subset of the phase space is called invariant if it consists of complete trajectories.) If a semi-trajectory is bounded, then its limit set is connected.
If 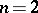 , that is, when the phase space is a plane, Poincaré (see ) and I. Bendixson (see [11]) have given an exhaustive description of the possible arrangements of the trajectories. Under the hypothesis that the equation
, that is, when the phase space is a plane, Poincaré (see ) and I. Bendixson (see [11]) have given an exhaustive description of the possible arrangements of the trajectories. Under the hypothesis that the equation 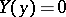 has only a finite number of solutions in any bounded part of the plane, they proved that the limit set of any bounded semi-trajectory can only be one of the following three types: 1) a single equilibrium state; 2) a single closed trajectory; or 3) a finite number of equilibrium states and trajectories converging to these equilibrium states as
has only a finite number of solutions in any bounded part of the plane, they proved that the limit set of any bounded semi-trajectory can only be one of the following three types: 1) a single equilibrium state; 2) a single closed trajectory; or 3) a finite number of equilibrium states and trajectories converging to these equilibrium states as 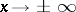 . Poincaré
. Poincaré
and A. Denjoy [12] considered the case of a first-order equation of the type (4) whose right-hand side is periodic in both arguments 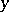 and
and  . Such equations are conveniently considered on a torus (see Differential equations on a torus). The structure of the solutions in this case depends essentially on the rotation number, defined by the formula
. Such equations are conveniently considered on a torus (see Differential equations on a torus). The structure of the solutions in this case depends essentially on the rotation number, defined by the formula
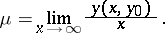 |
If 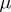 is rational, then there exists a periodic solution; if
is rational, then there exists a periodic solution; if 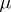 is irrational, then all solutions are quasi-periodic functions with two frequencies.
is irrational, then all solutions are quasi-periodic functions with two frequencies.
For 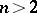 it is not possible to give such a clear description of the behaviour of the trajectories. There is, however, a lot of information about the limiting behaviour of higher-dimensional autonomous systems. Thus there are the following results, due to Birkhoff. Let a closed bounded invariant set of the phase space be called minimal if it contains no proper subset with the same properties. Then each minimal set is the closure of a recurrent trajectory. Thus, the limit set of each bounded semi-trajectory contains a recurrent trajectory.
it is not possible to give such a clear description of the behaviour of the trajectories. There is, however, a lot of information about the limiting behaviour of higher-dimensional autonomous systems. Thus there are the following results, due to Birkhoff. Let a closed bounded invariant set of the phase space be called minimal if it contains no proper subset with the same properties. Then each minimal set is the closure of a recurrent trajectory. Thus, the limit set of each bounded semi-trajectory contains a recurrent trajectory.
In the important particular case when the system has an invariant measure, the study of general regularity of the behaviour of the solutions has been carried out in great detail (see [5], [22]).
Of special interest for applications are structurally-stable systems (cf. Rough system), i.e. systems which are stable under a perturbation of the right-hand sides which is small in the sense of 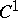 . For
. For 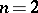 , A.A. Andronov and L.S. Pontryagin [13] stated necessary and sufficient conditions for structural stability. In particular, they showed that in any bounded part of the plane there are only a finite number of periodic solutions. For
, A.A. Andronov and L.S. Pontryagin [13] stated necessary and sufficient conditions for structural stability. In particular, they showed that in any bounded part of the plane there are only a finite number of periodic solutions. For 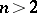 the behaviour of a structurally-stable system is considerably more complicated. S. Smale [14] has given an example of a structurally-stable system having an infinite number of periodic solutions in a bounded part of the phase space.
the behaviour of a structurally-stable system is considerably more complicated. S. Smale [14] has given an example of a structurally-stable system having an infinite number of periodic solutions in a bounded part of the phase space.
Numerous investigations have been devoted to the study of global properties of concrete systems of differential equations. In connection with investigations in the theory of automatic control, a new branch of the qualitative theory of differential equations evolved in the 1950s, namely the theory of stability of motion in the large. An important role in the theory of oscillations is played by dissipative systems: systems of the form (4) for which all solutions fall into some bounded domain as time increases. The properties of dissipative systems have been studied in great detail. Relatively reliable methods have been constructed enabling one to establish the dissipativeness of concrete systems (see [15]).
One of the problems in the qualitative theory of differential equations is that of the existence of periodic solutions. For the proof of the existence of such solutions use is often made of topological devices, in particular the various criteria for the existence of a fixed point. Many theorems of this sort have been proved by applying (generalizations of) the Poincaré–Birkhoff geometric principle.
A complete qualitative study of non-linear systems of differential equations has only been achieved in very special cases. For example, it has been proved (see [16]) that the Liénard equation
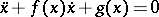 |
has, under very natural hypotheses, a unique periodic solution, while all its other solutions converge to this periodic one.
With regard to the van der Pol equation with perturbation,
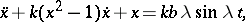 |
the following interesting facts have been established for large values of the parameter 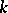 (in addition to a number of other results, see [17]). For a special choice of the parameter
(in addition to a number of other results, see [17]). For a special choice of the parameter  the equation has two asymptotically-stable solutions with periods
the equation has two asymptotically-stable solutions with periods 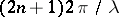 and
and 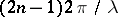 , where
, where  is a sufficiently large integer, and the "majority" of remaining solutions converge to these two. In addition, there is a countable set of unstable periodic solutions and a continuum of recurrent non-periodic ones.
is a sufficiently large integer, and the "majority" of remaining solutions converge to these two. In addition, there is a countable set of unstable periodic solutions and a continuum of recurrent non-periodic ones.
Local theory.
The qualitative investigation of the non-linear system (4) is considerably simplified if it only has to be conducted in a neighbourhood of a given solution, rather than on the whole 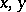 space. In this case, a simple change of variables reduces the problem to the study of the following system of differential equations:
space. In this case, a simple change of variables reduces the problem to the study of the following system of differential equations:
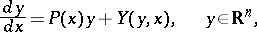 | (6) |
where the vector function 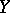 is, in a certain sense, small in comparison with
is, in a certain sense, small in comparison with 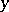 . The study of the behaviour of the solutions of (6) in a neighbourhood of the equilibrium state
. The study of the behaviour of the solutions of (6) in a neighbourhood of the equilibrium state 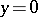 is in fact the subject matter of the local qualitative theory of differential equations.
is in fact the subject matter of the local qualitative theory of differential equations.
The problems of stability of the zero solution of (6) are central in this theory. The zero solution is called stable if the solution 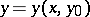 is continuous with respect to
is continuous with respect to 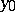 at
at 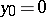 uniformly for
uniformly for 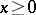 .
.
In the local qualitative theory of differential equations the case investigated most fully is that when the matrix 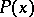 is constant. The problem of investigating a neighbourhood of the equilibrium states and the periodic solutions of an autonomous system reduces to this case.
is constant. The problem of investigating a neighbourhood of the equilibrium states and the periodic solutions of an autonomous system reduces to this case.
The description of the behaviour of the solutions of (6) in a neighbourhood of 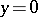 is relatively simple if
is relatively simple if 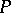 is constant and all its eigen values have non-zero real parts. In this case the matter reduces to the following fundamental result of Lyapunov–Perron (see , [18]). Suppose that
is constant and all its eigen values have non-zero real parts. In this case the matter reduces to the following fundamental result of Lyapunov–Perron (see , [18]). Suppose that 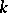 eigen values of the constant matrix
eigen values of the constant matrix 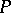 have negative real parts, while the remaining
have negative real parts, while the remaining 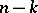 have positive real parts. Then there exists in the
have positive real parts. Then there exists in the 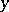 -space two manifolds
-space two manifolds 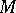 and
and 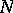 of dimensions
of dimensions 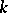 and
and 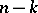 , respectively, such that if
, respectively, such that if 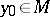 , then
, then 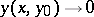 as
as 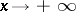 , and if
, and if 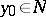 , then
, then 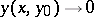 as
as 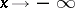 ; all the remaining solutions leave a neighbourhood of the origin as
; all the remaining solutions leave a neighbourhood of the origin as  increases or as
increases or as  decreases. The case when
decreases. The case when 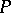 has eigen values with zero real parts is called critical.
has eigen values with zero real parts is called critical.
Lyapunov gave an exhaustive description of the behaviour of the solutions of (6) in a neighbourhood of the origin if the constant matrix 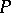 has one zero or two purely-imaginary eigen values, all the remaining eigen values have negative real parts, and the vector function
has one zero or two purely-imaginary eigen values, all the remaining eigen values have negative real parts, and the vector function 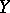 does not depend on
does not depend on  and is analytic (see [3]). The basic results in the local qualitative theory of autonomous second-order systems are due to Poincaré , Lyapunov [3], [4], Bendixson [11], and M. Frommer [19].
and is analytic (see [3]). The basic results in the local qualitative theory of autonomous second-order systems are due to Poincaré , Lyapunov [3], [4], Bendixson [11], and M. Frommer [19].
Consider the system of equations
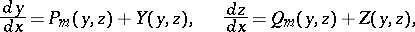 | (7) |
where 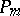 ,
, 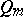 are forms of degree
are forms of degree 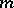 and the functions
and the functions 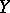 and
and 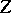 are small in comparison with
are small in comparison with 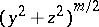 . Suppose that the equilibrium state, situated at the origin, is isolated. Then in the system (7) there either exists a solution converging to the origin or there exists a closed trajectory in every neighbourhood of the origin. In the second case, either all trajectories in a neighbourhood of the origin are closed (arrangement of centre type), or in any neighbourhood of the origin there are closed and non-closed trajectories (centre-focus type arrangement). It has been shown that for analytic
. Suppose that the equilibrium state, situated at the origin, is isolated. Then in the system (7) there either exists a solution converging to the origin or there exists a closed trajectory in every neighbourhood of the origin. In the second case, either all trajectories in a neighbourhood of the origin are closed (arrangement of centre type), or in any neighbourhood of the origin there are closed and non-closed trajectories (centre-focus type arrangement). It has been shown that for analytic 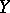 and
and 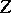 the centre-focus arrangement is not possible (see [20]).
the centre-focus arrangement is not possible (see [20]).
Furthermore, if a trajectory converges to the origin, then either it has a tangent at the origin, or the polar angle along it is unbounded. In the latter case the arrangement is of focus type. Only straight lines on which the quantity 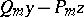 vanishes can be tangents to trajectories converging to the origin. Such lines are called exceptional directions. For sufficiently smooth
vanishes can be tangents to trajectories converging to the origin. Such lines are called exceptional directions. For sufficiently smooth 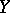 and
and 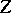 , algorithms have been developed allowing one to determine the existence and the number of trajectories entering the origin along a given exceptional direction. This enables one, in those cases when there exist trajectories entering the origin with a well-defined tangent, to describe completely the behaviour of the trajectories in a neighbourhood of the origin.
, algorithms have been developed allowing one to determine the existence and the number of trajectories entering the origin along a given exceptional direction. This enables one, in those cases when there exist trajectories entering the origin with a well-defined tangent, to describe completely the behaviour of the trajectories in a neighbourhood of the origin.
If the exceptional directions are missing or if all the solutions "pass them by" (that is, there are no trajectories entering the origin with a well-defined tangent), then the centre and focus problem arises.
Dependence of the behaviour of solutions on parameters of the system.
One of the central problems of the qualitative theory of differential equations is that of the behaviour of solutions of a system near to a given one, under the hypothesis that the properties of the latter are known. Consider the system
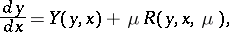 | (8) |
where 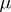 is a parameter. Suppose that the generating system, that is, the system (8) for
is a parameter. Suppose that the generating system, that is, the system (8) for 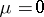 , possesses some property. The question is posed whether this property is preserved for small
, possesses some property. The question is posed whether this property is preserved for small 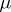 . A classical example of such a problem is the Poincaré problem (see [2]) on the existence of periodic solutions. Suppose that the vectors
. A classical example of such a problem is the Poincaré problem (see [2]) on the existence of periodic solutions. Suppose that the vectors 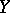 and
and 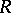 have period
have period 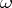 with respect to
with respect to  and that the generating system has an
and that the generating system has an 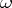 -periodic solution. In this case the problem reduces to the study of the quasi-linear system
-periodic solution. In this case the problem reduces to the study of the quasi-linear system
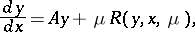 | (9) |
where 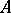 is a constant matrix. It turns out that if the eigen values of
is a constant matrix. It turns out that if the eigen values of 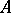 are distinct from
are distinct from 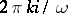 , where
, where 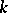 is an integer, then (9) has, for sufficiently small
is an integer, then (9) has, for sufficiently small 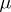 , a unique
, a unique 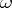 -periodic solution
-periodic solution 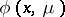 , continuous in
, continuous in 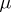 and with
and with 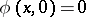 . If
. If 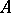 has eigen values of the form
has eigen values of the form 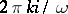 , the question of the existence and the number of periodic solutions depends essentially on the form of the perturbation
, the question of the existence and the number of periodic solutions depends essentially on the form of the perturbation 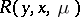 . In the solution of the problem of the existence of periodic solutions for this case the method of averaging proves to be extremely useful (see Krylov–Bogolyubov method of averaging).
. In the solution of the problem of the existence of periodic solutions for this case the method of averaging proves to be extremely useful (see Krylov–Bogolyubov method of averaging).
Similar questions can be posed for other types of solutions: bounded, recurrent, almost-periodic, etc. For example, if the vector 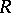 is uniformly almost-periodic in
is uniformly almost-periodic in  and if all eigen values of
and if all eigen values of 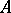 have non-zero real parts, then for sufficiently small
have non-zero real parts, then for sufficiently small 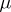 , (9) has a unique almost-periodic solution (see [21]).
, (9) has a unique almost-periodic solution (see [21]).
The method of the small parameter (cf. Small parameter, method of the) is also used to study questions of existence of integral sets for the system (8) with specified properties. From this point of view N.N. Bogolyubov (see [21]) has considered the following system, which is important for applications:
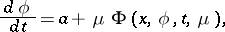 | (10) |
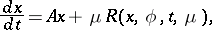 |
where  is a
is a 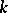 -dimensional,
-dimensional,  is an
is an  -dimensional and
-dimensional and  is a constant
is a constant 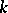 -dimensional vector, and all eigen values of the constant matrix
-dimensional vector, and all eigen values of the constant matrix 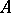 have non-zero real parts. The vectors
have non-zero real parts. The vectors 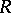 and
and 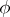 have period
have period 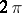 in the components of the vector
in the components of the vector 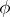 . When
. When 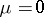 , the system (10) has the integral surface
, the system (10) has the integral surface 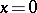 . Bogolyubov proved that for sufficiently small
. Bogolyubov proved that for sufficiently small 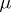 (10) has an integral surface
(10) has an integral surface
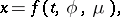 |
where 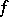 has period
has period 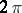 in the components of
in the components of 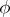 and
and 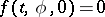 . Furthermore, if
. Furthermore, if 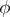 and
and 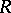 are
are 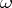 -periodic in
-periodic in 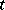 , then so is
, then so is 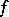 . If all eigen values of
. If all eigen values of 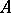 have negative real parts, then the integral surface
have negative real parts, then the integral surface 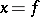 is asymptotically stable. If follows, in particular, that if in the system (8) the vector
is asymptotically stable. If follows, in particular, that if in the system (8) the vector 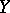 does not depend on
does not depend on  , and if for
, and if for 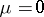 this system has a periodic solution which is asymptotically stable in the first approximation, then for sufficiently small
this system has a periodic solution which is asymptotically stable in the first approximation, then for sufficiently small 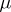 the system (8) has in the
the system (8) has in the 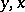 space a two-dimensional asymptotically-stable cylindrical integral manifold.
space a two-dimensional asymptotically-stable cylindrical integral manifold.
References
| [1a] | H. Poincaré, "Mémoire sur les courbes définiés par une équation différentielle" J. de Math. , 7 (1881) pp. 375–422 |
| [1b] | H. Poincaré, "Mémoire sur les courbes définiés par une équation différentielle" J. de Math. , 8 (1882) pp. 251–296 |
| [1c] | H. Poincaré, "Mémoire sur les courbes définiés par une équation différentielle" J. de Math. , 1 (1885) pp. 167–244 |
| [1d] | H. Poincaré, "Mémoire sur les courbes définiés par une équation différentielle" J. de Math. , 2 (1886) pp. 151–217 |
| [2] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 1–3 , Blanchard (1987) |
| [3] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [4] | A.M. Lyapunov, Mat. Sb. , 17 : 2 (1893) pp. 253–333 |
| [5] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) |
| [6] | G.D. Birkhoff, "Surface transformations and their dynamical applications" Acta Math. , 43 (1920) pp. 1–119 |
| [7] | N.P. Erugin, "Reducible systems" , Moscow-Leningrad (1946) (In Russian) |
| [8] | N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian) |
| [9] | M.G. Floquet, "Sur les équations différentielles linéaires à coefficients périodiques" Ann. Sci. Ecole Norm. Sup. Sér. 2 , 12 (1883) pp. 47–89 |
| [10] | J.Ch. Sturm, "Sur les équations linéaires du second ordre" J. Math. Pures et Appl. , 1 (1836) pp. 106–186 |
| [11] | I. Bendixson, "Sur les courbes définies par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88 |
| [12] | A. Denjoy, "Sur les courbes définies par les équations différentielles à la surface du tore" J. Math. Pures et Appl. Sér. 9 , 11 : 3 (1932) pp. 333–375 |
| [13] | A.A. Andronov, L.S. Pontryagin, "Systèmes grossiers" Dokl. Akad. Nauk SSSR , 14 : 5 (1937) pp. 247–250 |
| [14] | S. Smale, "Differentiable dynamical systems" Bull. Amer. Math. Soc. , 73 (1967) pp. 747–817 |
| [15] | V.A. Pliss, "Nonlocal problems of the theory of oscillations" , Acad. Press (1966) (Translated from Russian) |
| [16] | N. Levinson, O.K. Smith, "A general equation for relaxation oscillations" Duke Math. J. , 9 : 2 (1942) pp. 382–403 |
| [17] | J.E. Littlewood, "On nonlinear differential equations of the second order III: The equation 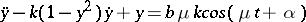 for large for large 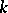 and its generalizations" Acta Math. , 97 : 3–4 (1957) pp. 267–308 and its generalizations" Acta Math. , 97 : 3–4 (1957) pp. 267–308 |
| [18] | O. Perron, "Ueber Stabilität und asymptotisches Verhalten der Integrale von Differentialgleichungenssysteme" Math. Z. , 29 (1928) pp. 129–160 |
| [19] | M. Frommer, Uspekhi Mat. Nauk , 9 (1941) pp. 212–253 |
| [20] | H. Dulac, "Sur les cycles limites" Bull. Soc. Math. France , 51 (1923) pp. 45–188 |
| [21] | N.N. Bogolyubov, "On certain statistical methods in mathematical physics" , Kiev (1945) (In Russian) |
| [22] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [23] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) |
| [24] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [25] | S. Lefschetz, "Differential equations: geometric theory" , Interscience (1957) |
Comments
For non-linear systems depending on a parameter vector 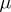 ,
,
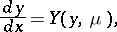 |
the occurrence of limit sets and their type as a function of 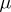 is studied in bifurcation theory. In addition to the branching of solutions of the stationary equation (the equilibria) one may also analyze periodic, quasi-periodic and chaotic solutions. At a bifurcation point a new limit set may branch off, and limit sets may turn from stable to unstable or vice versa, see [a1]. A new development in the qualitative theory of differential equations is the transition to a normal form. Near an equilibrium or a periodic solution one can develop the right-hand side of the equation into a power series. Making a truncation one can transform the system to one of the standard forms, which are classified in the way of the elementary catastrophes, see [a2]. Furthermore, the analysis of trajectories near an equilibrium can be restricted to the ones forming a manifold which in the equilibrium is tangent to the eigen space of eigen values with vanishing real parts. This approach is called the centre manifold theory, see [a3]. The discovery of chaotic dynamics of non-linear systems has brought new elements in the theory of differential equations. For the existence of non-periodic solutions of a van der Pol type of equation with a periodic forcing see [a4]. For dissipative systems, stable non-periodic limit sets exist, known as strange attractors (cf. Strange attractor), see [a5]. For a general introduction into the qualitative theory of ordinary differential equations see [a6].
is studied in bifurcation theory. In addition to the branching of solutions of the stationary equation (the equilibria) one may also analyze periodic, quasi-periodic and chaotic solutions. At a bifurcation point a new limit set may branch off, and limit sets may turn from stable to unstable or vice versa, see [a1]. A new development in the qualitative theory of differential equations is the transition to a normal form. Near an equilibrium or a periodic solution one can develop the right-hand side of the equation into a power series. Making a truncation one can transform the system to one of the standard forms, which are classified in the way of the elementary catastrophes, see [a2]. Furthermore, the analysis of trajectories near an equilibrium can be restricted to the ones forming a manifold which in the equilibrium is tangent to the eigen space of eigen values with vanishing real parts. This approach is called the centre manifold theory, see [a3]. The discovery of chaotic dynamics of non-linear systems has brought new elements in the theory of differential equations. For the existence of non-periodic solutions of a van der Pol type of equation with a periodic forcing see [a4]. For dissipative systems, stable non-periodic limit sets exist, known as strange attractors (cf. Strange attractor), see [a5]. For a general introduction into the qualitative theory of ordinary differential equations see [a6].
References
| [a1] | S.-N. Chow, J.K. Hale, "Methods of bifurcation theory" , Springer (1982) |
| [a2] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Springer (1983) (Translated from Russian) |
| [a3] | J. Carr, "Applications of centre manifold theory" , Springer (1981) |
| [a4] | M. Levi, "Qualitative analysis of the periodically forced relaxation oscillations" Memoires Amer. Math. Soc. , 244 (1981) |
| [a5] | J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983) |
| [a6] | F. Verhulst, "Nonlinear differential equations and dynamical systems" , Springer (1990) |
| [a7] | D.V. Anosov (ed.) V.I. Arnol'd (ed.) , Dynamical systems , I: Ordinary differential equations and smooth dynamical systems , Springer (1988) (Translated from Russian) |
| [a8] | V.I. Arnol'd, "Dynamical systems" , III , Springer (1988) (Translated from Russian) |
| [a9] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
Qualitative theory of differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Qualitative_theory_of_differential_equations&oldid=12023