Quadric
A quadric is a surface of the second order. In a three-dimensional (projective, affine or Euclidean) space a quadric is a set of points whose homogeneous coordinates  (with respect to a projective, affine or Cartesian system of coordinates) satisfy a homogeneous equation of degree two:
(with respect to a projective, affine or Cartesian system of coordinates) satisfy a homogeneous equation of degree two:
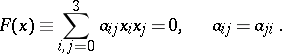 |
The bilinear symmetric form
 |
is called the polar form relative to  . Two points
. Two points  ,
,  at which
at which  are called conjugate points with respect to the quadric. If the line
are called conjugate points with respect to the quadric. If the line  intersects the quadric at the points
intersects the quadric at the points  and the points
and the points 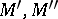 are conjugate to each other with respect to the quadric, then
are conjugate to each other with respect to the quadric, then  and
and  form a harmonic quadruple. The points of a quadric and only these are self-conjugate. A line all points of which lie on a quadric is called a generator of the quadric. By the pole of a given plane with respect to a quadric is meant the point that is conjugate to every point of this plane. The set of points in the space that are conjugate to a given point
form a harmonic quadruple. The points of a quadric and only these are self-conjugate. A line all points of which lie on a quadric is called a generator of the quadric. By the pole of a given plane with respect to a quadric is meant the point that is conjugate to every point of this plane. The set of points in the space that are conjugate to a given point  with respect to a quadric is called the polar of
with respect to a quadric is called the polar of  with respect to the quadric. A tangent plane to a quadric is the polar of the point of contact. The polar of a point
with respect to the quadric. A tangent plane to a quadric is the polar of the point of contact. The polar of a point  is defined by the linear equation
is defined by the linear equation  with respect to the coordinates
with respect to the coordinates 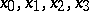 . If
. If  , then the polar of
, then the polar of 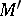 is a plane; if
is a plane; if  , then the polar of
, then the polar of  is the whole space. In this case
is the whole space. In this case  belongs to the quadric and is called a singular point of it. If
belongs to the quadric and is called a singular point of it. If  , then the quadric has no singular points and is called a non-degenerate quadric. In projective space this is an imaginary ovaloid, a real ovaloid or a ruled quadric. A non-degenerate quadric determines a correlation (or polarity), i.e. a bijective mapping from the set of points of projective space onto the set of planes. A ruled non-degenerate quadric has two distinct families of generators, distributed on the quadric so that any two lines of the same family are non-intersecting, while two lines of different families intersect at one point. If
, then the quadric has no singular points and is called a non-degenerate quadric. In projective space this is an imaginary ovaloid, a real ovaloid or a ruled quadric. A non-degenerate quadric determines a correlation (or polarity), i.e. a bijective mapping from the set of points of projective space onto the set of planes. A ruled non-degenerate quadric has two distinct families of generators, distributed on the quadric so that any two lines of the same family are non-intersecting, while two lines of different families intersect at one point. If  , then a quadric is a cone (real or imaginary) with vertex at the unique singular point. A real cone has a single family of generators, passing through its vertex. If
, then a quadric is a cone (real or imaginary) with vertex at the unique singular point. A real cone has a single family of generators, passing through its vertex. If  , then the quadric splits into a pair of planes (real or imaginary), intersecting in a line consisting of its singular points. If
, then the quadric splits into a pair of planes (real or imaginary), intersecting in a line consisting of its singular points. If  , then a quadric is a double real plane consisting of singular points. The affine properties of a quadric are distinguished by its behaviour with respect to the plane at infinity,
, then a quadric is a double real plane consisting of singular points. The affine properties of a quadric are distinguished by its behaviour with respect to the plane at infinity,  . For example, an ellipsoid (hyperboloid, paraboloid) is a non-degenerate quadric that does not intersect (does intersect, is tangent to) the plane at infinity. The centre of a quadric is the pole of the plane at infinity, a diameter is a line through the centre.
. For example, an ellipsoid (hyperboloid, paraboloid) is a non-degenerate quadric that does not intersect (does intersect, is tangent to) the plane at infinity. The centre of a quadric is the pole of the plane at infinity, a diameter is a line through the centre.
References
| [1] | S.P. Finikov, "Analytic geometry" , Moscow (1952) (In Russian) |
| [2] | N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian) |
Comments
References
| [a1] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 65–94 |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a3] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a4] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [a5] | H.F. Baker, "Principles of geometry" , 3. Solid gometry , Cambridge Univ. Press (1961) |
A quadric in algebraic geometry is a projective algebraic variety defined by a homogeneous quadratic equation
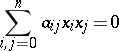 |
in the projective space  over a ground field
over a ground field  .
.
Suppose further that the ground field is algebraically closed and has characteristic not equal to 2. Let 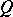 be a quadric in
be a quadric in  and let
and let  be the set of its singular points. Then
be the set of its singular points. Then  is the empty set if and only if
is the empty set if and only if  , where
, where  is the rank of the corresponding quadratic form. If
is the rank of the corresponding quadratic form. If 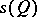 is non-empty, then
is non-empty, then  is a cone over a non-degenerate quadric of dimension
is a cone over a non-degenerate quadric of dimension  whose vertex is the projective subspace
whose vertex is the projective subspace  in
in  of dimension
of dimension 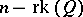 . All quadrics with
. All quadrics with 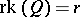 are projectively equivalent to the quadric
are projectively equivalent to the quadric
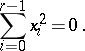 |
Let 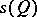 be empty and let
be empty and let  be a linear subspace of maximal dimension (it is called a generator of the quadric
be a linear subspace of maximal dimension (it is called a generator of the quadric 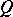 ). Then
). Then
a) if  , then
, then 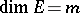 ;
;
b) if 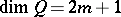 , then
, then  .
.
Furthermore, the family of all subspaces  of maximal dimension on
of maximal dimension on  is a closed non-singular subset
is a closed non-singular subset  of the Grassmann manifold of subspaces of dimension
of the Grassmann manifold of subspaces of dimension 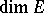 in
in  . If
. If  ,
,  ,
, 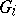 ,
,  , are non-intersecting non-singular irreducible rational varieties of the same dimension
, are non-intersecting non-singular irreducible rational varieties of the same dimension
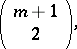 |
while  and
and 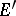 belong to the same component if and only if
belong to the same component if and only if
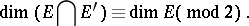 |
If 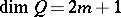 , then
, then  is a non-singular irreducible rational variety of dimension
is a non-singular irreducible rational variety of dimension
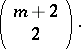 |
In case  is empty and
is empty and 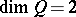 ,
, 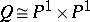 ; if
; if 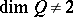 , then
, then  (where Pic denotes the Picard group).
(where Pic denotes the Picard group).
Every quadric is rational: A birational isomorphism of a quadric  with a projective space is determined by stereographic projection of the quadric
with a projective space is determined by stereographic projection of the quadric 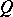 from some point
from some point  ,
,  . Varieties that are complete intersections of quadrics have been studied from the point of view of birational geometry [3]. Intersections of two quadrics are studied in [2], of three in [4].
. Varieties that are complete intersections of quadrics have been studied from the point of view of birational geometry [3]. Intersections of two quadrics are studied in [2], of three in [4].
Any projective variety  can be imbedded in a projective space
can be imbedded in a projective space 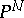 (for sufficiently large
(for sufficiently large  ) so that its image is the intersection (generally incomplete) of the quadrics containing it [1].
) so that its image is the intersection (generally incomplete) of the quadrics containing it [1].
The study of quadrics over non-closed fields is closely related to the arithmetic of quadratic forms.
References
| [1] | D. Mumford, "Varieties defined by quadratic equations" , Questions on algebraic varieties, C.I.M.E. Varenna, 1969 , Cremonese (1970) pp. 29–100 |
| [2] | M. Reid, "The complete intersection of two or more quadrics" (1972) (Ph.D. Thesis) |
| [3] | V.S. [V.S. Ryaben'kii] Rjabenki, A.F. [A.F. Filippov] Filipov, "Über die stabilität von Differenzgleichungen" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
| [4] | A.N. Tyurin, "On the intersection of quadrics" Russian Math. Surveys , 30 : 6 (1975) pp. 51–106 Uspekhi Mat. Nauk , 30 : 6 (1975) pp. 51–99 |
V.A. Iskovskikh
Comments
References
| [a1] | P. Griffiths, S. Harris, "Principles of algebraic curves" , Wiley (1978) |
| [a2] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , II , Cambridge Univ. Press (1952) |
| [a3] | H. Lenz, "Vorlesungen über projektive Geometrie" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1965) |
| [a4] | G. Pickert, "Analytische Geometrie" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1953) |
| [a5] | R. Donagi, "Group law on the intersection of two quadrics" Ann. Sc. Norm. Sup. Pisa Ser. IV , 7 (1980) pp. 217–240 |
| [a6] | I.Y. Mérirdol, "Théorème de Torelli affine pour les intersections de deux quadriques" Invent. Math. , 80 (1985) pp. 375–416 |
Quadric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadric&oldid=11769