Difference between revisions of "Quadratic form"
m (fixing spaces) |
m (remove . in titles) |
||
| Line 11: | Line 11: | ||
{{TEX|done}} | {{TEX|done}} | ||
| − | ''over a commutative ring $ R $ | + | ''over a commutative ring $ R $ with an identity'' |
| − | with an identity'' | ||
A homogeneous polynomial | A homogeneous polynomial | ||
| Line 164: | Line 163: | ||
denotes transposition). | denotes transposition). | ||
| − | ==Algebraic theory of quadratic forms | + | ==Algebraic theory of quadratic forms== |
This is the theory of quadratic forms over fields. | This is the theory of quadratic forms over fields. | ||
| Line 265: | Line 264: | ||
The algebraic theory of quadratic forms has been generalized [[#References|[7]]] to the case of a field of characteristic 2. | The algebraic theory of quadratic forms has been generalized [[#References|[7]]] to the case of a field of characteristic 2. | ||
| − | ==Arithmetic theory of quadratic forms | + | ==Arithmetic theory of quadratic forms== |
This is the theory of quadratic forms over rings. | This is the theory of quadratic forms over rings. | ||
| Line 346: | Line 345: | ||
as well as "precise" formulas for certain concrete quadratic forms. | as well as "precise" formulas for certain concrete quadratic forms. | ||
| − | ==Analytic theory of quadratic forms | + | ==Analytic theory of quadratic forms== |
Analytic methods were brought into the theory of quadratic forms by P.G.L. Dirichlet. Developing these methods, C.L. Siegel arrived at general formulas for the number of representations of a form by genera of forms. | Analytic methods were brought into the theory of quadratic forms by P.G.L. Dirichlet. Developing these methods, C.L. Siegel arrived at general formulas for the number of representations of a form by genera of forms. | ||
| Line 516: | Line 515: | ||
even, see [[#References|[24]]].) | even, see [[#References|[24]]].) | ||
| − | ==Geometric theory of quadratic forms | + | ==Geometric theory of quadratic forms== |
For the study of such questions in the theory of quadratic forms as reduction theory, automorphisms and arithmetic minima of quadratic forms, the method of continuous parameters was developed by Ch. Hermite, which thereupon became an extensive branch of the theory of quadratic forms, namely the geometric theory of quadratic forms, or the geometry of quadratic forms (which can also be regarded as part of the [[Geometry of numbers|geometry of numbers]]). The idea of the method consists in the following. With a given $ n $-dimensional point lattice $ \Lambda $ | For the study of such questions in the theory of quadratic forms as reduction theory, automorphisms and arithmetic minima of quadratic forms, the method of continuous parameters was developed by Ch. Hermite, which thereupon became an extensive branch of the theory of quadratic forms, namely the geometric theory of quadratic forms, or the geometry of quadratic forms (which can also be regarded as part of the [[Geometry of numbers|geometry of numbers]]). The idea of the method consists in the following. With a given $ n $-dimensional point lattice $ \Lambda $ | ||
some kind of arithmetical quantity $ a = a ( \Lambda ) $ | some kind of arithmetical quantity $ a = a ( \Lambda ) $ | ||
Latest revision as of 08:08, 12 August 2022
over a commutative ring $ R $ with an identity
A homogeneous polynomial
$$ q = q ( x) = q ( x _ {1}, \dots, x _ {n} ) = \ \sum _ {i < j } q _ {ij} x _ {j} x _ {i} ,\ \ 1 \leq i \leq j \leq n , $$
in $ n = n ( q) $ variables with coefficients $ q _ {ij} \in R $. Usually $ R $ is the field $ \mathbf C $, $ \mathbf R $ or $ \mathbf Q $, or else the ring $ \mathbf Z $, the ring of integer elements of an algebraic number field or the ring of integers of the completion of an algebraic number field with respect to a non-Archimedian norm.
The symmetric square matrix $ A = A ( q) = ( a _ {ij} ) $ of order $ n $, where $ a _ {ii} = 2 q _ {ii} $, $ a _ {ij} = a _ {ji} = q _ {ij} $, $ 1 \leq i \leq j \leq n $, is called the Kronecker matrix of the quadratic form $ q ( x) $; in Siegel's notation: $ q ( x) = ( 1/2) A [ x] $. If the discriminant $ D ( q) $ of the quadratic form $ q $ is non-zero, then $ q $ is said to be a non-degenerate quadratic form, while if it is zero, $ q $ is called degenerate.
A quadratic form $ q ( x) $ is called Gaussian if it can be expressed in symmetric notation:
$$ q ( x) = \sum _ {i , j = 1 } ^ { n } b _ {ij} x _ {i} x _ {j} ,\ \ b _ {ij} = b _ {ji} \in R , $$
that is, there exist $ b _ {ij} = b _ {ji} \in R $ for which $ q _ {ij} = 2 b _ {ij} $, $ 1 \leq i \leq j \leq n $. The symmetric square matrix $ B = B ( q) = ( b _ {ij} ) $ is called the matrix (or Gaussian matrix) of the quadratic form $ q ( x) $. The quantity $ d = d ( q) = \mathop{\rm det} B $ is called the determinant of $ q ( x) $; in this connection,
$$ D ( q) = ( - 1 ) ^ {n/2} 2 ^ {n} d ( q) \ \ \textrm{ if } n ( q) \textrm{ is even } , $$
$$ D ( q) = ( - 1 ) ^ {( n - 1 ) / 2 } 2 ^ {n- 1} d ( q) \ \textrm{ if } n ( q) \textrm{ is odd } . $$
If $ R $ is a field of characteristic distinct from 2, then every quadratic form over $ R $ is Gaussian. If $ R $ is imbeddable in a field $ F $ of characteristic distinct from 2, then a quadratic form $ q ( x) $ over $ R $ can be regarded as Gaussian, but with matrix $ B = B ( q) $ over $ F $ and $ d ( q) \in F $.
Two quadratic forms $ q _ {1} $ and $ q _ {2} $ are equivalent over $ R $ ($ q _ {1} \simeq q _ {2} $ $ ( R) $) if one can be obtained from the other by an invertible (with respect to $ R $) linear homogeneous change of variables, that is, if they have congruent matrices: there exists an invertible square matrix $ U $ over $ R $ such that $ A ( q _ {1} ) = U ^ {T} A ( q _ {2} ) U $. The collection of quadratic forms over $ R $ equivalent over $ R $ to a given one is called the class of that quadratic form. The discriminant of the quadratic form is, up to the square of an invertible element in $ R $, an invariant of the class.
Another way of looking at quadratic forms is the following. Let $ V $ be a unital $ R $-module; a mapping $ q : V \rightarrow R $ is called a quadratic mapping (or a quadratic form) on the module $ V $ if 1) $ q ( a x ) = a ^ {2} q ( x) $, $ a \in R $, $ x \in V $; and 2) the mapping $ b _ {q} : V \times V \rightarrow R $ given by
$$ b _ {q} ( x , y ) = q ( x + y ) - q ( x) - q ( y) $$
is a bilinear form on $ V $. The pair $ ( V , q ) $ is called a quadratic module. The form $ b _ {q} $ is always symmetric.
To each bilinear form $ b ( x , y ) $ on $ V $ corresponds the quadratic form $ q ( x) = q _ {b} ( x) = b ( x , x ) $; here $ b _ {q _ {b} } ( x , y ) = b ( x , y ) + b ( y , x ) $.
If in the ring $ R $ the element 2 has an inverse, then $ q \iff b _ {q} / 2 $ is a one-to-one correspondence between the quadratic and symmetric forms on $ V $. If $ V $ is a free $ R $-module of rank $ n $ and $ q $ is a quadratic form on $ V $, then to each basis $ e _ {1}, \dots, e _ {n} $ of $ V $ corresponds a quadratic form in the classical sense,
$$ q ( x _ {1}, \dots, x _ {n} ) = q ( x _ {1} e _ {1} + \dots + x _ {n} e _ {n} ) = \ \sum _ {1 \leq i \leq j \leq n } q _ {ij} x _ {i} x _ {j} , $$
where $ q _ {ii} = q ( e _ {i} ) $, $ q _ {ij} = b _ {q} ( e _ {i} , e _ {j} ) $, $ 1 \leq i \leq j \leq n $. Every quadratic form $ q ( x _ {1}, \dots, x _ {n} ) $ over $ R $ is obtained in this way from some quadratic module $ ( R ^ {n} , q ) $, and conversely. Under a change of basis the quadratic form $ q ( x _ {1}, \dots, x _ {n} ) $ is converted to an equivalent one.
An element $ \gamma \in R $ is said to be representable by the quadratic form $ q $ (or one says that the form $ q $ represents $ \gamma $) if $ \gamma $ is the value of this form for certain values of the variables. Equivalent quadratic forms represent the same elements. A quadratic form $ q ( x) $ over an ordered field $ R $ is called indefinite if it represents both positive and negative elements, and positive (negative) definite if $ q ( x) > 0 $ (respectively $ q ( x) < 0 $) for all $ x \neq 0 $. A non-degenerate quadratic form which represents 0 non-trivially is called isotropic, otherwise it is called anisotropic. Similarly, a quadratic form $ r ( y _ {1}, \dots, y _ {m} ) $ is called representable by a quadratic form $ q $ if $ q $ can be converted to $ r $ by a substitution of certain linear forms in $ y _ {1}, \dots, y _ {m} $ for the variables in $ q $; that is, if there is a rectangular $ ( m \times n ) $ matrix $ S $ over $ R $ such that $ A ( r) = S ^ {T} A ( q) S $ (there $ {} ^ {T} $ denotes transposition).
Algebraic theory of quadratic forms
This is the theory of quadratic forms over fields.
Let $ F $ be an arbitrary field of characteristic distinct from 2. The problem of representing a form $ r $ by a form $ q $ over $ F $ reduces to the problem of equivalence of forms, because (Pall's theorem) in order that a non-degenerate quadratic form $ r $ be representable by a non-degenerate quadratic form $ q $ over $ F $, it is necessary and sufficient that there exist a form $ h = h ( x _ {m+1}, \dots, x _ {n} ) $ such that $ r \dot{+} h $ and $ q $ are equivalent over $ F $. Here $ r \dot{+} h $ is the orthogonal direct sum of forms, that is, $ r $ and $ h $ have no variables in common.
Witt's cancellation theorem. If $ h \dot{+} q _ {1} \simeq h \dot{+} q _ {2} $, then $ q _ {1} \simeq q _ {2} $.
Every quadratic form over $ F $ is equivalent to a diagonal one:
$$ a _ {1} x _ {1} ^ {2} + \dots + a _ {r} x _ {r} ^ {2} + \dots + a _ {n} x _ {n} ^ {2} . $$
It will be assumed that $ a _ {1}, \dots, a _ {r} \neq 0 $ and $ a _ {r+ 1} = \dots = a _ {n} = 0 $. The number $ r $ is called the rank of $ q $, which is the same as the rank of the matrix $ A ( q) $. If every element of $ F $ has a square root, then a quadratic form over $ F $ is equivalent to the form $ x _ {1} ^ {2} + \dots + x _ {r} ^ {2} $ (the normal form of a quadratic form).
Every non-degenerate quadratic form $ q $ is equivalent to a form
$$ q ^ \prime = q _ {0} + \sum _ { i= 1} ^ { k } ( x _ {i} ^ {2} - y _ {i} ^ {2} ) , $$
where $ q _ {0} $ is anisotropic; here $ q $ uniquely determines $ k $ and the class of the form $ q _ {0} $ over $ F $, called the anisotropic kernel of $ q $ (see also Witt decomposition). Two forms $ q _ {1} $ and $ q _ {2} $ having the same anisotropic kernel are called similar in the sense of Witt. A ring structure can be defined on the classes of similar forms (see Witt ring).
Let $ F $ be an ordered field (in particular the field $ \mathbf R $) and suppose that every positive element of $ F $ is a square. Then every quadratic form $ q $ is reducible to the form
$$ x _ {1} ^ {2} + \dots + x _ {s} ^ {2} - x _ {s+ 1} ^ {2} - \dots - x _ {r- s} ^ {2} . $$
Here the numbers $ s $ and $ r - s $ (the positive and negative indices of inertia) are uniquely determined by the form (see Law of inertia). Thus, for these fields the problem of equivalence of quadratic forms is solved.
The problem of equivalence over the field $ \mathbf Q $ reduces to the analogous problem for $ p $-adic number fields: In order that $ q _ {1} $ and $ q _ {2} $ be equivalent over $ \mathbf Q $, it is necessary and sufficient that $ q _ {1} $ and $ q _ {2} $ be equivalent over $ \mathbf Q _ {p} $ for all primes $ p $ and over $ \mathbf Q _ \infty = \mathbf R $ (the Minkowski–Hasse theorem). A similar assertion holds for $ A $-fields — algebraic number fields and fields of algebraic functions in one variable over a finite field of constants. This is a particular case of the Hasse principle. In the field $ \mathbf Q _ {p} $ ($ p \neq \infty $) the problem of equivalence is solved by means of the Hasse invariant.
A quadratic form $ q $ over a field $ F $ is called multiplicative over $ F $ if
$$ q ( x _ {1}, \dots, x _ {n} ) q ( y _ {1}, \dots, y _ {n} ) = q ( z _ {1}, \dots, z _ {n} ) , $$
where the $ z _ {i} $ are rational functions of $ x _ {1}, \dots, x _ {n} $, $ y _ {1}, \dots, y _ {n} $ over $ F $. If, in addition, the $ z _ {i} $ are bilinear functions, then the form is said to have a composition. Composition is possible only for the cases $ n = 2 , 4 , 8 $ (Hurwitz's theorem). There is a simple description of multiplicative forms [16].
The algebraic theory of quadratic forms has been generalized [7] to the case of a field of characteristic 2.
Arithmetic theory of quadratic forms
This is the theory of quadratic forms over rings.
This theory arose in connection with problems of solving Diophantine equations of the second degree. The question of solving such equations reduces to the problem of representing integers by an integral quadratic form $ q $, that is, the problem of solving the equation $ b = q ( x _ {1}, \dots, x _ {n} ) $ in $ \mathbf Z $. Algorithms are known which reduce the determination (description) of all solutions of this equation to the problem of equivalence of quadratic forms over $ \mathbf Z $, that is, the problem of finding for given quadratic forms $ q ( x) =( 1/2) A [ x] $ and $ q _ {1} ( x) =( 1/2) A _ {1} [ x] $ invertible matrices $ U $ over $ \mathbf Z $ such that $ U ^ {T} A U = A _ {1} $. For $ n = 2 $ such algorithms were constructed by J.L. Lagrange and C.F. Gauss, who created the general theory of binary quadratic forms (cf. Binary quadratic form). They were generalized to arbitrary $ n $ by H. Smith and H. Minkowski.
One of the central problems of the arithmetic theory is that of finding simple criteria for the existence of representations $ S $ of a form $ r ( x) = ( 1/2) B [ x] $ by a form $ q ( x) =( 1/2) A [ x] $, that is, criteria for the solutions of the matrix equation
$$ \tag{1 } S ^ {T} A S = B , $$
and also the problem of constructing a formula for the number $ R ( q , r ) = R ( A , B ) $ of such representations. In this connection, if the number of representations is infinite, then it becomes a question of the number $ R ^ \prime ( q , r ) $ of "essentially different" representations. (Two representations $ S $ and $ S ^ \prime $ are identified if $ S ^ \prime = S V $, where $ V $ is an integral automorphism of $ q $, that is, $ V ^ {T} A V = A $.) A necessary condition for the existence of representations is the solvability of (1) over $ \mathbf R $ and the solvability over $ \mathbf Z $ of the matrix congruence
$$ \tag{2 } S ^ {T} A S \equiv B ( \mathop{\rm mod} g ) $$
for any $ g $. (For the solvability of all congruences (2) it is sufficient that (2) be solvable for $ g = g _ {0} = 8 D ( q) D ( r) $.) These necessary conditions, called "generic conditions for the solvability of a matrix equationgeneric" , are equivalent to the solvability of (1) over $ \mathbf Z _ {p} $ for every prime $ p $ and over $ \mathbf Z _ \infty = \mathbf R $. They are also equivalent to the solvability of (1) over the field of rationals $ \mathbf Q $" without an essential denominator", that is, the existence of a rational solution $ S $ with common denominator coprime to any pre-assigned integer $ g $ (it being sufficient to confine oneself to $ g = g _ {0} $). The solvability conditions of (2) can be expressed in terms of generic invariants of $ q $ and $ r $. The number of solutions of (2) is found by means of Gauss sums.
The genus of a quadratic form over $ \mathbf Z $ is the set of quadratic forms over $ \mathbf Z $ equivalent to one another over $ \mathbf Z _ {p} $ for all primes $ p $, including $ \mathbf Z _ \infty = \mathbf R $. The genus of a quadratic form consists of a finite number of classes with the same discriminant. The genus of a quadratic form $ q ( x) =( 1/2) A [ x] $ can be given by a finite number of generic invariants — order invariants expressed in terms of the elementary divisors of A — and characters of the form $ \chi ( q) = \pm 1 $. The genus can also be given by the values of Gauss sums. An important role in the theory of quadratic forms is also played by the notion of a spinor genus, a more delicate notion than that of a genus.
The number $ R ^ \prime ( q , r ) $ of essentially different representations of the form $ r $ by the form $ q $ is in a simple way related to the number $ R _ {0} ^ \prime ( q , r ) $ of essentially different primitive representations, that is, representations $ S $ such that the greatest common divisor of the $ m $-th order minors (cf. Minor) of the matrix is 1. For the quantity
$$ S _ {0} ( q , r ) = \sum _ { i= 1} ^ { l } R _ {0} ^ \prime ( q _ {i} , r ) $$
(the averaging function of $ R _ {0} ^ \prime ( q , r ) $ over the genus of $ q $), where $ q _ {1}, \dots, q _ {l} $ are representatives of all classes of the genus of $ q $ (one from each class), there are formulas (see [11], [15]) expressing $ S _ {0} ( q , r ) $ in terms of the number of solutions of certain congruences. In case the genus of $ q $ consists of a single class, these formulas completely solve the question of the number of representations. In the case of genera having several classes, only asymptotic formulas are known for $ R ( q , r ) $, as well as "precise" formulas for certain concrete quadratic forms.
Analytic theory of quadratic forms
Analytic methods were brought into the theory of quadratic forms by P.G.L. Dirichlet. Developing these methods, C.L. Siegel arrived at general formulas for the number of representations of a form by genera of forms.
Let $ q ( x _ {1}, \dots, x _ {n} ) = ( 1/2) A [ x ] $ and $ r ( x _ {1}, \dots, x _ {m} ) =( 1/2) B [ x ] $ be positive-definite quadratic forms over $ \mathbf Z $.
The number
$$ \widetilde{R} ( q , r ) = \ \frac{1}{M ( q) } \sum _ { i= 1} ^ { l } \frac{R ( q _ {i} , r ) }{E ( q _ {i} ) } $$
is called the Siegel mean with respect to the genus for the number of representations $ R ( q , r ) $ of the form $ r $ by the form $ q $. Here $ E ( q _ {i} ) $ is the number of automorphisms of $ q _ {i} $ and
$$ M ( q) = \ \sum _ { i= 1} ^ { l } \frac{1}{E ( q _ {i} ) } $$
is the weight of the genus of $ q $. Let
$$ \chi _ \infty ( q , r ) = \ \lim\limits _ {\theta \rightarrow r } \ \frac{V ( \theta ^ \prime ) }{V ( \theta ) } , $$
where $ \theta $ is a neighbourhood of $ r = r ( x) $ in the $ m ( m + 1 ) / 2 $-dimensional space of $ m $-ary quadratic forms over $ \mathbf R $, $ \theta ^ \prime $ is the corresponding domain of solutions $ S _ {1} $ of the matrix equation (1) over $ \mathbf R $, and $ V ( \theta ) $ and $ V ( \theta ^ \prime ) $ are their volumes.
Siegel's formula for the quadratic forms $ q $ and $ r $ is
$$ \tag{3 } \widetilde{R} ( q , r ) = \ \tau \chi _ \infty ( q , r ) H ( q , r ) , $$
where $ \tau = 1 / 2 $ if $ n = m > 1 $ or $ n = m + 1 $, and $ \tau = 1 $ otherwise. Here
$$ H ( q , r ) = \ \lim\limits _ {g \rightarrow \infty } \ \frac{R _ {g} ( q , r ) }{2 ^ {\omega _ {n- m} ( g) } g ^ {n m - m ( m + 1 ) / 2 } } , $$
where the limit is taken over those sequences of $ g $'s for which any natural number is a divisor of almost-all terms of $ g $, $ \omega _ {0} ( g) $ is the number of distinct prime divisors of $ g $, $ \omega _ {n- m} ( g) = 0 $ if $ n > m $, and $ R _ {g} ( q , r ) $ is the number of representations of $ r $ by $ q $, that is, the number of solutions of the matrix congruence
$$ S ^ {T} \left ( \frac{1}{2} A \right ) S = \frac{1}{2} B ( \mathop{\rm mod} g ) . $$
The following formula holds:
$$ H ( q , r ) = \ \frac{R _ {g _ {0} } ( q , r ) }{2 ^ {\omega _ {n- m} ( g _ {0} ) } g _ {0} ^ {n m - m ( m + 1 ) / 2 } } ,\ \ g _ {0} = 8 D ( q) D ( r) . $$
There are a number of equivalent definitions for $ H ( q , r ) $ and an expression (see [17]) in terms of generalized Gauss sums. Formula (3) includes as a special case Minkowski's formula for the weight of the genus:
$$ M ( q) = \ \frac{2 ( d ( q) ) ^ {( n + 1 ) / 2 } }{\pi ^ {n ( n + 1 ) / 2 } } \frac{\prod _ { k= 1} ^ { n } \Gamma ( k / 2 ) }{\prod _ { p } \chi _ {p} ( q , q ) } ,\ \ n > 1 . $$
For the case $ n = 2 $ the latter gives the Dirichlet formula for the number of classes.
Formulas analogous to (3) hold also for indefinite forms and forms with integral algebraic coefficients (see [17], [18]).
An application of the theory of the number of representations of numbers by positive quadratic forms in an even number of variables has been given by E. Hecke [10]. The theory of modular forms (cf. Modular form) enables one to obtain formulas for $ R ( q , b ) $ (see the survey [5]).
The circle method (see [4]) has been applied to the question of the representation of numbers by quadratic forms in four or more variables. If $ q $ is a positive-definite quadratic form over $ \mathbf Z $, then for $ n \geq 4 $ an application of the circle method leads to the asymptotic formula
$$ R ( q , b ) = \ \frac{\pi ^ {n / 2 } b ^ {n / 2 - 1 } }{\Gamma ( n / 2 ) d ( q) } H ( q , b ) + O ( b ^ {( n - 1 ) / 4 + \epsilon } ) . $$
Similar asymptotic formulas can also be obtained by the circle method for indefinite quadratic forms with $ n \geq 4 $.
For the investigation of $ R ( q , b ) $ in the case $ n = 3 $, Linnik's discrete ergodic method (cf. Linnik discrete ergodic method) has been applied (see [3], [4]). It is based on the fact that on some set of representations of numbers by ternary quadratic forms, an ergodic flow of the representations can be constructed which is regulated by an operator connected with the problem of the representation of numbers by quaternary quadratic forms. The ergodic method leads (under certain necessary conditions) to an estimate of the type
$$ R ( q , b ) > c h ( - \Delta b ) ,\ \ c = c ( q) > 0 ; $$
and in a number of cases asymptotic formulas have also been obtained.
Recent results of H. Iwaniec [22] concerning means of Kloosterman sums lead to the asymptotic formula [23]
$$ R( q, b) = \frac{\pi ^ {n/2} b ^ {n/2-} 1 }{\Gamma ( n/2) d( q) } H( q , b) + O ( b ^ {( n- 1)/4 - 1/28 + \epsilon } ) , $$
where $ b $ is square-free (or where the square-free part of $ b $ is bounded). This formula is non-trivial already for $ n \geq 3 $. This formula provides an approach to a conjecture of H. Petersson. (The Petersson conjecture has already been proved by P. Deligne for $ n $ even, see [24].)
Geometric theory of quadratic forms
For the study of such questions in the theory of quadratic forms as reduction theory, automorphisms and arithmetic minima of quadratic forms, the method of continuous parameters was developed by Ch. Hermite, which thereupon became an extensive branch of the theory of quadratic forms, namely the geometric theory of quadratic forms, or the geometry of quadratic forms (which can also be regarded as part of the geometry of numbers). The idea of the method consists in the following. With a given $ n $-dimensional point lattice $ \Lambda $ some kind of arithmetical quantity $ a = a ( \Lambda ) $ is associated and the behaviour of the function $ a = a ( \Lambda ) $ is considered under small changes of the parameters of $ \Lambda $. A characteristic feature of the geometry of quadratic forms is the systematic use of the $ n ( n + 1 ) / 2 $-dimensional coefficient (parameter) space, in which the lattice $ \Lambda $ is represented by a point. Let
$$ f = \sum _ {i , j = 1 } ^ { n } a _ {ij} x _ {i} x _ {j} $$
be a quadratic form with real coefficients $ a _ {ij} = a _ {ji} $ ($ i , j = 1, \dots, n $). Associated with $ f $ is the point $ \widetilde{f} = ( a _ {11}, \dots, a _ {nn} , a _ {12}, \dots, a _ {n- 1},n ) $ in $ N $-dimensional Euclidean space (where $ N = n ( n + 1 ) / 2 $), called the coefficient space. Then corresponding to the positive-definite form $ f $ is an open convex cone $ \mathfrak P $ with vertex at the origin, called the cone of positivity. The lattice $ \Lambda $ is related to the class of equivalent $ n $-ary positive-definite quadratic forms; by means of a basis $ [ \overline{a} _ {1} \dots \overline{a} _ {n} ] $ of $ \Lambda $, the form
$$ f = \sum _ {i , j = 1 } ^ { n } ( \overline{a} _ {i} \overline{a} _ {j} ) x _ {i} x _ {j} $$
is associated with it. Thus, an infinite discrete set of points of $ \mathfrak P $ has been associated with $ \Lambda $. If one chooses the correct domain of reduction $ \mathfrak F \subset \mathfrak P $ of positive-definite quadratic forms, then each lattice is uniquely associated with a point $ \widetilde{f} \in \mathfrak F $ of the coefficient space. Small changes in the point $ \widetilde{f} $ correspond to small changes in the parameters of $ \Lambda $.
The geometric theory of quadratic forms divides up into a number of fairly independent theories related by a single method of investigation. At its foundation is the reduction theory of positive quadratic forms, which, by studying the domains of reduction $ \mathfrak F $, solves the problem of the equivalence of positive quadratic forms, one of the central problems in the arithmetical theory of quadratic forms (see Quadratic forms, reduction of).
An essential role is played by the theory of Voronoi lattice types. It has important applications in the theory of parallelohedra. The theory of types has found application in the solution of problems on the most economic lattice covering of an $ n $-dimensional space by balls.
Another traditional branch of the geometric theory of quadratic forms is the theory of perfect forms, also created by G.F. Voronoi. This theory allows one to solve the Hermite problem on the arithmetical minima of positive quadratic forms; this is equivalent to the problem on the densest lattice packing of balls in an $ n $-dimensional space. The problem on the densest lattice packing of balls and that of the most economic lattice covering by balls are the best known examples of the extremal problems which constitute a significant part of the geometry of quadratic forms.
Also related to the geometric theory of quadratic forms are certain generalizations of the continued fractions algorithm; for example, the algorithm of Voronoi for calculating the units of a cubic field, and the theory of fundamental domains of automorphisms of indefinite quadratic forms.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) MR0195803 Zbl 0145.04902 |
| [2a] | B.N. Delone, "The geometry of positive definite quadratic forms" Uspekhi Mat. Nauk , 3 (1937) pp. 16–62 (In Russian) |
| [2b] | B.N. Delone, "The geometry of positive definite quadratic forms" Uspekhi Mat. Nauk , 4 (1938) pp. 102–164 (In Russian) |
| [3] | Yu.V. Linnik, "Ergodic properties of algebraic fields" , Springer (1968) (Translated from Russian) MR0238801 Zbl 0162.06801 |
| [4] | A.V. Malyshev, "On the representation of integers by positive quadratic forms" , Moscow-Leningrad (1962) (In Russian) Zbl 0425.10024 Zbl 0163.04604 |
| [5] | A.V. Malyshev, "On formulas for the representation of numbers by positive quadratic forms (problems)" , Current problems in analytic number theory , Minsk (1974) pp. 119–137 (In Russian) |
| [6] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) MR0344216 Zbl 0256.12001 |
| [7] | C. Arf, "Untersuchungen über quadratischen Formen in Körpern der Characteristik 2, I" J. Reine Angew. Math. , 183 (1941) pp. 148–167 |
| [8] | M. Eichler, "Quadratische Formen und orthogonale Gruppen" , Springer (1952) MR0051875 Zbl 0049.31106 |
| [9a] | H. Hasse, "Ueber die Darstellbarkeit von Zahlen durch quadratische Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 129–148 Zbl 49.0102.01 |
| [9b] | H. Hasse, "Ueber die Aequivalenz quadratischer Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 205–224 Zbl 49.0102.02 |
| [9c] | H. Hasse, "Symmetrische Matrizen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 153 (1924) pp. 12–43 Zbl 49.0104.01 |
| [9d] | H. Hasse, "Zur Theorie des quadratischen Hilbertschen Normenrestsymbols in algebraischen Körper" J. Reine Angew. Math. , 153 (1924) pp. 76–93 |
| [9e] | H. Hasse, "Darstellbarkeit von Zahlen durch quadratische Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 113–130 Zbl 49.0114.01 |
| [9f] | H. Hasse, "Aequivalenz quadratischer Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 158–162 Zbl 50.0104.03 |
| [9g] | H. Hasse, "Zur Theorie des Hilbertschen Normenrestsymbols in algebraischen Zahlkörpern" J. Reine Angew. Math. , 153 (1924) pp. 184–191 Zbl 50.0105.01 |
| [9h] | H. Hasse, "Das allgemeine Reziprocitätsgesetz und seine Ergänzungssätze in beliebigen Zahlkörpern für gewisse nicht-primäre Zahlen" J. Reine Angew. Math. , 153 (1924) pp. 192–207 |
| [10] | E. Hecke, "Mathematische Werke" , Vandenhoeck & Ruprecht (1959) MR0104550 Zbl 0092.00102 |
| [11] | B.W. Jones, "The arithmetic theory of quadratic forms" , Math. Assoc. Amer. (1950) MR0037321 Zbl 0041.17505 |
| [12] | T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973) MR0396410 Zbl 0259.10019 |
| [13] | H. Minkowski, "Gesammelte Abhandlungen" , 1–2 , Teubner (1911) Zbl 42.0023.03 |
| [14] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1963) Zbl 0107.03301 |
| [15] | G. Pall, "Representation by quadratic forms" Canad. J. Math. , 1 (1949) pp. 344–364 MR0034795 Zbl 0034.02201 |
| [16] | A. Pfister, "Multiplikative quadratische Formen" Arch. Math. , 16 (1965) pp. 363–370 MR0184937 Zbl 0146.26001 |
| [17] | C.L. Siegel, "Lectures on quadratic forms" , Tata Inst. (1963) MR0271028 Zbl 0115.04401 |
| [18] | C.L. Siegel, "Gesammelte Abhandlungen" , 1–4 , Springer (1966–1979) MR0543842 MR0197270 Zbl 0402.01011 Zbl 0143.00101 |
| [19] | H.J.S. Smith, "The collected mathematical papers" , 1–2 , Chelsea, reprint (1965–1979) Zbl 25.0029.02 |
| [20] | G.L. Watson, "Integral quadratic forms" , Cambridge Univ. Press (1960) MR0118704 Zbl 0090.03103 |
| [21] | O.M. Fomenko, "Applications of the theory of modular forms to number theory" J. Soviet Math. , 14 : 4 (1980) pp. 1307–1362 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 15 (1977) pp. 5–91 MR0491505 Zbl 0446.10021 |
| [22] | H. Iwaniec, "Fourier coefficients of modular forms of half-integral weight" Invent. Math. , 87 (1987) pp. 385–401 MR0870736 Zbl 0606.10017 |
| [23] | W. Duke, Sém. Théorie des Nombres de Bordeaux , 37 (1987–1988) pp. 1–7 |
| [24] | E. Freitag, R. Kiehl, "Etale cohomology and the Weil conjecture" , Springer (1988) (Translated from German) MR0926276 Zbl 0643.14012 |
Comments
Recent accounts of the geometric theory of quadratic forms are contained in [a4]. There Dirichlet–Voronoi cells, parallelohedra, reduction theory, and relations to the problem of densest lattice packing and of thinnest lattice covering with Euclidean balls are discussed in detail.
References
| [a1] | B.N. Delone, S.S. Ryshkov, "Extremal problems in the theory of positive quadratic forms" Proc. Steklov Inst. Math. , 112 (1971) pp. 211–231 Trudy Mat. Inst. Steklov. , 112 (1971) pp. 203–223 MR340183 Zbl 0261.10020 |
| [a2] | P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) MR1003606 Zbl 0683.10025 |
| [a3] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) MR0893813 Zbl 0611.10017 |
| [a4] | C.L. Siegel, "Lectures on the geometry of numbers" , Springer (1989) MR1020761 Zbl 0691.10021 |
| [a5] | S.S. Ryshkov, E.P. Baranovskii, "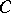 -types of -types of  -dimensional lattices and 5-dimensional primitive parallelohedra" , Amer. Math. Soc. (1978) (Translated from Russian) -dimensional lattices and 5-dimensional primitive parallelohedra" , Amer. Math. Soc. (1978) (Translated from Russian) |
| [a6] | J.W.S. Cassels, "Rational quadratic forms" , Acad. Press (1978) MR0522835 Zbl 0395.10029 |
Quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadratic_form&oldid=51969