Ptolemeus theorem
From Encyclopedia of Mathematics
In every convex quadrangle inscribed in a circle, the product of the lengths of the diagonals is equal to the sum of the products of the lengths of its opposite sides. It is called after Claudius Ptolemeus (2nd century), who used it to deduce certain trigonometric relations.
Comments
One also encounters Ptolemy's theorem. Ptolemy's theorem is equivalent to the formula for 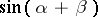 .
.
The converse to Ptolemy's theorem is also true. If in a convex quadrangle the product of the lengths of the diagonals is equal to the sum of the products of the lengths of its opposite sides, the four vertices are lying on a circle.
References
| [a1] | H.S.M. Coxeter, S.L. Greitzer, "Geometry revisited" , Math. Assoc. Amer. (1967) |
| [a2] | E.A. Maxwell, "Geometry by transformations" , Cambridge Univ. Press (1975) |
| [a3] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
How to Cite This Entry:
Ptolemeus theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ptolemeus_theorem&oldid=18608
Ptolemeus theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ptolemeus_theorem&oldid=18608
This article was adapted from an original article by P.S. Modenov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article