Pseudo-prime
Traditionally, a composite natural number  is called a pseudo-prime if
is called a pseudo-prime if  modulo
modulo  , for it has long been known that primes have this property. (The term is apparently due to D.H. Lehmer.) There are infinitely many such
, for it has long been known that primes have this property. (The term is apparently due to D.H. Lehmer.) There are infinitely many such  , the first five being
, the first five being
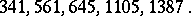 |
More recently, the concept has been extended to include any composite number that acts like a prime in some realization of a probabilistic primality test. That is, it satisfies some easily computable necessary, but not sufficient, condition for primality. Pseudo-primes in this larger sense include:
1) ordinary base- pseudo-primes, satisfying
pseudo-primes, satisfying  modulo
modulo  ;
;
2) Euler base-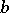 pseudo-primes, whose Jacobi symbol with
pseudo-primes, whose Jacobi symbol with 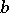 satisfies
satisfies
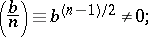 |
3) strong base-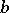 pseudo-primes, for which the sequence
pseudo-primes, for which the sequence 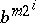 modulo
modulo  ,
,  , is either always
, is either always  , or contains
, or contains 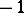 . (Here
. (Here  with
with 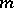 odd.)
odd.)
For each 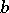 , the implications 3)
, the implications 3)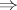 2)
2)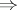 1) hold. A number
1) hold. A number  that is an ordinary base-
that is an ordinary base-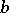 pseudo-prime for all
pseudo-prime for all 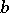 prime to
prime to  is called a Carmichael number. Analogous numbers for the other two categories do not exist.
is called a Carmichael number. Analogous numbers for the other two categories do not exist.
For a thorough empirical study of pseudo-primes, see [a4]. Lists of pseudo-primes to various small bases can be found in [a6].
The concept of a pseudo-prime has been generalized to include primality tests based on finite fields and elliptic curves (cf. also Finite field; Elliptic curve). For reviews of this work, see [a3], [a5].
The complementary concept is also of interest. The base 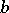 is called a (Fermat) witness for
is called a (Fermat) witness for  if
if  is composite but not a base-
is composite but not a base-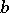 pseudo-prime. Euler and strong witnesses are similarly defined. If
pseudo-prime. Euler and strong witnesses are similarly defined. If 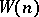 , the smallest strong witness for
, the smallest strong witness for  , grows sufficiently slowly, there is a polynomial-time algorithm for primality. It is known that
, grows sufficiently slowly, there is a polynomial-time algorithm for primality. It is known that 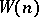 is not bounded [a2], but if an extended version of the Riemann hypothesis (cf. Riemann hypotheses) holds, then
is not bounded [a2], but if an extended version of the Riemann hypothesis (cf. Riemann hypotheses) holds, then 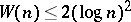 [a1].
[a1].
References
| [a1] | E. Bach, "Analytic methods in the analysis and design of number-theoretic algorithms" , MIT (1985) |
| [a2] | W.R. Alford, A. Granville, C. Pomerance, "On the difficulty of finding reliable witnesses" , Algorithmic Number Theory, First Internat. Symp., ANTS-I , Lecture Notes in Computer Science , 877 , Springer (1994) pp. 1–16 |
| [a3] | F. Morain, "Pseudoprimes: a survey of recent results" , Proc. Eurocode '92 , Springer (1993) pp. 207–215 |
| [a4] | C. Pomerance, J.L. Selfridge, S.S. Wagstaff, Jr., "The pseudoprimes to  " Math. Comp. , 35 (1980) pp. 1003–1026 " Math. Comp. , 35 (1980) pp. 1003–1026 |
| [a5] | P. Ribenboim, "The book of prime number records" , Springer (1989) (Edition: Second) |
| [a6] | N.J.A. Sloane, S. Plouffe, "The encyclopedia of integer sequences" , Acad. Press (1995) |
Pseudo-prime. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-prime&oldid=16100