Pseudo-local tomography
Let 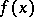 be a piecewise smooth, compactly supported function,
be a piecewise smooth, compactly supported function, 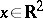 . The Radon transform
. The Radon transform 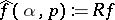 is defined by the formula
is defined by the formula 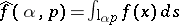 , where
, where 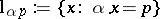 is a straight line parametrized by a unit vector
is a straight line parametrized by a unit vector 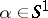 ,
, 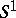 is the unit circle in
is the unit circle in 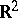 and
and 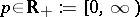 . By definition,
. By definition, 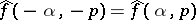 . By local tomographic data one means the values of
. By local tomographic data one means the values of 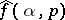 for
for 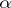 and
and 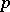 satisfying the condition
satisfying the condition 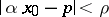 , where
, where 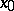 is a given point and
is a given point and 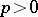 is a small number. Thus, local tomographic data are the line integrals of
is a small number. Thus, local tomographic data are the line integrals of 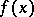 for the lines intersecting the "region of interest" , the disc centred at
for the lines intersecting the "region of interest" , the disc centred at 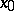 of radius
of radius 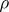 (cf. also Local tomography; Tomography).
(cf. also Local tomography; Tomography).
It is not possible, in general, to find  from the local tomographic data [a2]. What practically useful information about
from the local tomographic data [a2]. What practically useful information about 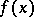 can one get from these data? Information, very useful practically, is the location of discontinuity curves of
can one get from these data? Information, very useful practically, is the location of discontinuity curves of 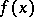 and the sizes of the jumps of
and the sizes of the jumps of 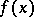 across these curves.
across these curves.
Pseudo-local tomography solves the problem of finding the above information from the local tomographic data.
This is done by computing the pseudo-local tomography function, introduced in [a2]:
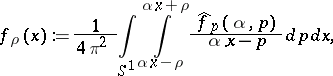 | (a1) |
where 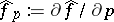 . The inversion formula reads:
. The inversion formula reads:
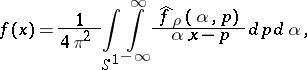 | (a2) |
so that (a1) is based on the following idea: Keep a small neighbourhood of the singular point 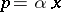 in (a1) and neglect the rest of the Cauchy integral in (a1).
in (a1) and neglect the rest of the Cauchy integral in (a1).
By definition, one needs only the local tomographic data to calculate the pseudo-local tomography function 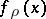 .
.
The basic result is: 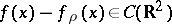 is a continuous function [a2], [a1].
is a continuous function [a2], [a1].
Therefore, 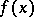 and
and 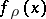 have the same discontinuity curves and the same sizes of the jumps across discontinuities.
have the same discontinuity curves and the same sizes of the jumps across discontinuities.
It is also proved in [a2] that if 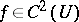 , where
, where 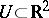 is an open set, then the function
is an open set, then the function 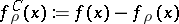 has the following properties:
has the following properties:
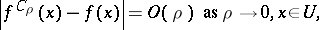 | (a3) |
and the convergence in (a3) is uniform on compact subsets of  . If
. If 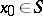 , where
, where 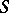 is a smooth discontinuity curve of
is a smooth discontinuity curve of 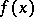 , then
, then
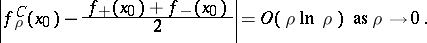 | (a4) |
Here,  are the limiting values of
are the limiting values of 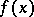 as
as  from different sides of
from different sides of 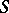 along a path non-tangential to
along a path non-tangential to 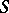 .
.
If 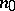 is a unit vector normal to
is a unit vector normal to 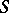 at the point
at the point 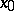 , then for an arbitrary
, then for an arbitrary 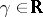 ,
, 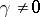 , one has
, one has
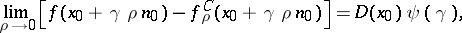 |
where
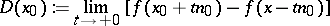 |
and
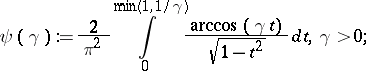 |
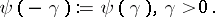 |
The function 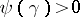 , is monotonically decreasing on
, is monotonically decreasing on 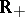 ,
, 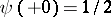 ,
,
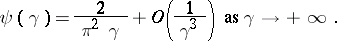 |
If 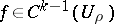 , for
, for  the
the 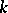 th order derivatives of
th order derivatives of 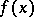 exist in
exist in 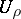 , some of them being discontinuous across
, some of them being discontinuous across 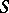 , and
, and  is piecewise-smooth in
is piecewise-smooth in 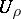 , then
, then 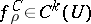 .
.
Other properties of 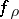 can be found in [a2], which also contains a general method for constructing a family of pseudo-local tomography functions, that is, functions which are computable from local tomographic data and having the same discontinuities and the same sizes of the jumps as
can be found in [a2], which also contains a general method for constructing a family of pseudo-local tomography functions, that is, functions which are computable from local tomographic data and having the same discontinuities and the same sizes of the jumps as 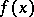 .
.
References
| [a1] | A.G. Ramm, A. Katsevich, "Pseudolocal tomography" SIAM J. Appl. Math. , 56 : 1 (1996) pp. 167–191 |
| [a2] | A.G. Ramm, A. Katsevich, "The Radon transform and local tomography" , CRC (1996) |
Pseudo-local tomography. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-local_tomography&oldid=12248