Proper morphism
A morphism of schemes that is separated, universally closed and of finite type. A morphism of schemes  is called closed if for any closed
is called closed if for any closed  the set
the set  is closed in
is closed in  , and universally closed if for any base change
, and universally closed if for any base change  the morphism
the morphism  is closed. The property of being a proper morphism is preserved under composition, base change and taking Cartesian products. Proper morphisms are closely related to projective morphisms: any projective morphism is proper, and a proper quasi-projective morphism is projective. Any proper morphism is dominated by a projective one (Chow's lemma). See also Complete algebraic variety; Projective scheme.
is closed. The property of being a proper morphism is preserved under composition, base change and taking Cartesian products. Proper morphisms are closely related to projective morphisms: any projective morphism is proper, and a proper quasi-projective morphism is projective. Any proper morphism is dominated by a projective one (Chow's lemma). See also Complete algebraic variety; Projective scheme.
Proper morphisms have a number of good cohomological properties. 1) If a morphism 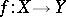 is proper and if
is proper and if  is a coherent sheaf of
is a coherent sheaf of  -modules, then for any
-modules, then for any 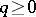 the sheaves of
the sheaves of 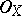 -modules
-modules  are coherent (the finiteness theorem). A similar fact holds for étale cohomology. In particular, if
are coherent (the finiteness theorem). A similar fact holds for étale cohomology. In particular, if 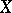 is a complete scheme over a field
is a complete scheme over a field 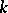 , then the cohomology spaces
, then the cohomology spaces  are finite-dimensional. 2) For any point
are finite-dimensional. 2) For any point 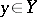 , the completion of the
, the completion of the 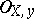 -module
-module  coincides with
coincides with
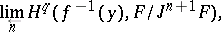 |
where 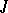 is the ideal of the subscheme
is the ideal of the subscheme  in
in 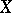 (the comparison theorem). 3) If
(the comparison theorem). 3) If 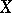 is a proper scheme over a complete local ring
is a proper scheme over a complete local ring  , then the categories of coherent sheaves on
, then the categories of coherent sheaves on 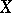 and on its formal completion
and on its formal completion 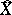 are equivalent (the algebraization theorem). There are analytic analogues of the first and third properties. For example (see [3]), for a complete
are equivalent (the algebraization theorem). There are analytic analogues of the first and third properties. For example (see [3]), for a complete 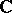 -scheme
-scheme  any coherent analytic sheaf on
any coherent analytic sheaf on 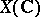 is algebraizable and
is algebraizable and
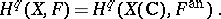 |
4) Let 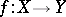 be a proper morphism, let
be a proper morphism, let 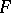 be a sheaf of finite Abelian groups in the étale topology of
be a sheaf of finite Abelian groups in the étale topology of 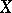 , and let
, and let 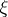 be a geometric point of the scheme
be a geometric point of the scheme 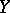 . Then the fibre of the sheaf
. Then the fibre of the sheaf 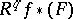 at
at 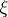 is isomorphic to
is isomorphic to  (the base-change theorem, see [2]).
(the base-change theorem, see [2]).
References
| [1] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" Publ. Math. IHES , 2–3 (1961–1963) |
| [2] | "Théorie des topos et cohomologie étale des schémas" M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , SGA 4 , Lect. notes in math. , 269; 270; 305 , Springer (1972–1973) |
| [3] | A. Grothendieck (ed.) et al. (ed.) , Revêtements étales et groupe fondamental. SGA 1 , Lect. notes in math. , 224 , Springer (1971) |
| [4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Comments
A morphism of schemes 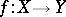 is locally of finite type if there exists a covering of
is locally of finite type if there exists a covering of  by affine open subschemes
by affine open subschemes 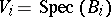 such that for each
such that for each 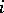 there is an open covering by affine subschemes
there is an open covering by affine subschemes 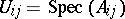 of
of  such that
such that 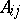 is a finitely-generated algebra over
is a finitely-generated algebra over 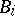 (with respect to the homomorphism of rings
(with respect to the homomorphism of rings  which defines
which defines  ). The morphism is of finite type if the coverings
). The morphism is of finite type if the coverings  of
of 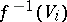 can be taken finite for all
can be taken finite for all 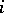 .
.
A morphism  is finite if there exists an affine open covering
is finite if there exists an affine open covering  ,
, 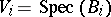 , of
, of 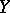 such that
such that 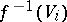 is affine for all
is affine for all  , say
, say 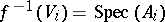 , and
, and 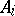 is a finitely-generated
is a finitely-generated  -module.
-module.
The analytic analogue of property 1) above is called Grauert's finiteness theorem, see Finiteness theorems.
In topology a mapping of topological spaces 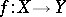 is said to be proper it for each topological space
is said to be proper it for each topological space 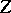 the mapping
the mapping  is closed. It follows that for every continuous mapping
is closed. It follows that for every continuous mapping  the base-change mapping
the base-change mapping 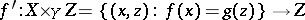 ,
, 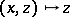 , is closed, so that a proper mapping of topological spaces is the same thing as a universally closed mapping. If
, is closed, so that a proper mapping of topological spaces is the same thing as a universally closed mapping. If 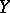 is locally compact, a continuous mapping
is locally compact, a continuous mapping 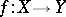 is proper if and only if the inverse image of each compact subset of
is proper if and only if the inverse image of each compact subset of  is compact. Sometimes this last property is taken as a definition.
is compact. Sometimes this last property is taken as a definition.
Let 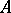 be a Noetherian ring which is complete (and separated) with respect to the
be a Noetherian ring which is complete (and separated) with respect to the 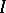 -adic topology on
-adic topology on 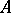 , i.e.
, i.e. 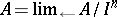 . On
. On 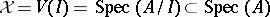 one defines a sheaf of topological rings
one defines a sheaf of topological rings 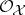 by
by 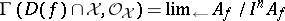 for
for  . The ringed space
. The ringed space  is called the formal spectrum of
is called the formal spectrum of  (with respect to
(with respect to 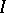 ). It is denoted by
). It is denoted by 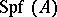 . A locally Noetherian formal scheme is, by definition, a topologically ringed space which is locally isomorphic to formal spectra of a Noetherian ring. Morphisms of formal schemes are morphisms of the corresponding topologically ringed spaces.
. A locally Noetherian formal scheme is, by definition, a topologically ringed space which is locally isomorphic to formal spectra of a Noetherian ring. Morphisms of formal schemes are morphisms of the corresponding topologically ringed spaces.
Let 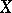 be a (locally) Noetherian scheme and
be a (locally) Noetherian scheme and 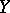 a closed subscheme defined by a sheaf of ideas
a closed subscheme defined by a sheaf of ideas  . The formal completion of
. The formal completion of 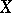 along
along 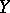 , denoted by
, denoted by 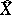 , is the topologically ringed space
, is the topologically ringed space 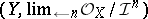 . It is a (locally) Noetherian formal scheme.
. It is a (locally) Noetherian formal scheme.
All this serves to state the following theorem, which is sometimes called the fundamental theorem on proper morphisms: Let  be a proper morphism of locally Noetherian schemes,
be a proper morphism of locally Noetherian schemes,  a closed subscheme,
a closed subscheme, 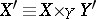 the inverse image of
the inverse image of  . Let
. Let  and
and 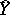 be the formal completions of
be the formal completions of 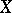 and
and 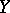 along
along 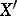 and
and 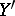 , respectively. Let
, respectively. Let 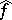 be the induced morphism of formal schemes
be the induced morphism of formal schemes  . Then, for every coherent
. Then, for every coherent  -module
-module 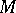 on
on  , there are canonical isomorphisms
, there are canonical isomorphisms
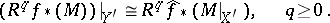 |
This theorem can be used to prove the Zariski connectedness theorem (cf. Zariski theorem).
References
| [a1] | N. Bourbaki, "Elements of mathematics. General topology" , Chapt. I, §10 , Addison-Wesley (1966) (Translated from French) |
Proper morphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Proper_morphism&oldid=13200