Prolongation of solutions of differential equations

The property of solutions of ordinary differential equations to be extendible to a larger interval of the independent variable. Let

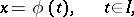(1)

be a solution of the system

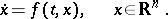(2)

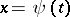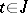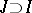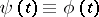A solution , , is called a prolongation of the solution (1) if and for .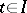

Suppose that the function

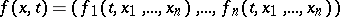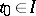is defined in a domain and suppose . The solution (1) is called indefinitely extendible (indefinitely extendible forwards (to the right), indefinitely extendible backward (to the left)) if a prolongation of it exists defined on the axis 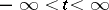(respectively, on the semi-axis 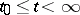, on the semi-axis 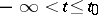). The solution (1) is called extendible forwards (to the right) up to the boundary 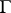of 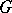if a prolongation 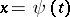, , 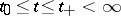of it exists with the following property: For any compact set 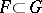there is a value 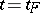, , 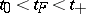such that the point 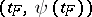does not belong to 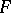. Extendibility backward (to the left) up to the boundary 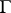is defined analogously. A solution that cannot be extended is called non-extendible.

If the function 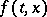is continuous in 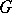, then every solution (1) of (2) can be either extended forwards (backward) or indefinitely or up to the boundary 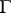. In other words, every solution of (2) can be extended to a non-extendible solution. If the partial derivatives

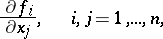(3)

are continuous in 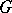, then such a prolongation is unique.

An interval 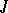is called a maximal interval of existence of a solution of (2) if the solution cannot be extended to a larger interval. For any solution of a linear system

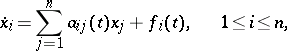with coefficients 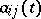and right-hand sides 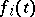, , 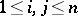that are continuous on an interval 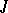, the maximal interval of existence of a solution coincides with 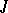. For solutions of a non-linear system the maximal intervals of existence may differ for different solutions, and determining them is a difficult task. E.g. for the solution to the Cauchy problem

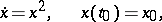one has

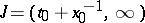if ,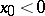

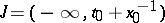if 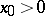, and

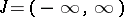if .

A sufficient condition under which one can indicate the maximal interval of existence of a solution is, e.g., Wintner's theorem: Suppose that the function 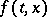is continuous for 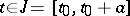, , and that it satisfies in this domain the estimate

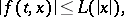where 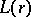is a function continuous for 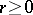, 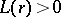and for some , ,

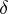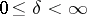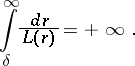Then every solution of (2) exists on the whole of .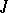

This theorem also holds for 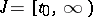. Sufficient conditions for indefinite extendibility of a solution are of great interest. E.g., if and its partial derivatives (3) are continuous for 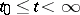, , and if for these values of 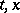the estimates

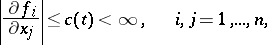hold, then the solution of (2) with 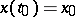exists for 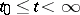, for any .

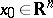Consider the Cauchy problem

(4)

for an autonomous system, where 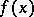is continuously differentiable in a domain 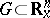. If, as grows, the phase trajectory of the solution 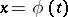of (4) remains in a compact subset 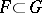, then this solution can be extended to the semi-axis .

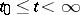References

[1]	L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)
[2]	V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian)
[3]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[4]	E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17
[5]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[6]	L. Cesari, "Asymptotic behavior and stability problems in ordinary differential equations" , Springer (1959)
[7]	A. Wintner, "The non-local existence problem of ordinary differential equations" Amer. J. Math. , 67 (1945) pp. 277–284

Comments

Instead of prolongation of solutions, continuation of solutions is nowadays mostly used.