Projective representations of symmetric and alternating groups
The classification of the projective representations of a finite group 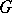 (cf. also Projective representation) was obtained by I. Schur [a9], [a10], who showed that over the complex field
(cf. also Projective representation) was obtained by I. Schur [a9], [a10], who showed that over the complex field 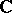 the problem of determining all projective representations of
the problem of determining all projective representations of 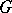 can be reduced to determining the linear representations of stem extensions
can be reduced to determining the linear representations of stem extensions 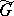 of
of 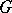 , called representation groups, by its Schur multiplier
, called representation groups, by its Schur multiplier  (cf. also Schur multiplicator). A standard reference is [a5].
(cf. also Schur multiplicator). A standard reference is [a5].
In the case of the symmetric groups  and the alternating groups
and the alternating groups 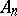 (cf. also Symmetric group; Alternating group), Schur [a11] further showed that
(cf. also Symmetric group; Alternating group), Schur [a11] further showed that
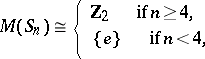 |
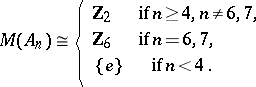 |
The representation groups are not unique, for 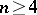 there are two for
there are two for 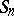 ; however, to determine the projective representations of
; however, to determine the projective representations of 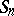 it suffices to consider one of these, which will be denoted by
it suffices to consider one of these, which will be denoted by 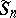 ; similarly,
; similarly, 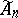 is a representation group of
is a representation group of 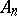 . The non-linear representations of
. The non-linear representations of  and
and  , that is, those representations
, that is, those representations 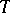 for which
for which  ,
, 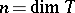 , where
, where  is the generator of
is the generator of  are called spin representations. Schur [a10] classified the complex irreducible spin representations of
are called spin representations. Schur [a10] classified the complex irreducible spin representations of 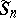 and
and  ,
, 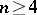 (and also the remaining non-linear projective representations for
(and also the remaining non-linear projective representations for 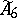 and
and  ). Although more complicated, the classification of the spin representations follows the corresponding results for the linear representations of these groups. (cf. Representation of the symmetric groups). A standard reference is [a4], but see also [a12].
). Although more complicated, the classification of the spin representations follows the corresponding results for the linear representations of these groups. (cf. Representation of the symmetric groups). A standard reference is [a4], but see also [a12].
In this case, the irreducible spin representations are parametrized by the set 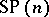 of strict partitions
of strict partitions 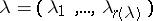 of
of  , where
, where  . If
. If 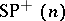 (respectively,
(respectively, 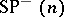 ) denotes the subset of
) denotes the subset of 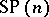 where the number of even parts is even (odd), then a complete list of irreducible spin representations is:
where the number of even parts is even (odd), then a complete list of irreducible spin representations is:
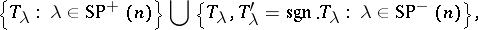 |
where  is the sign representation of
is the sign representation of 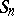 . The characters of these representations, called spin characters and denoted by
. The characters of these representations, called spin characters and denoted by 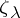 and
and 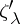 , can take only non-zero values on the classes of
, can take only non-zero values on the classes of 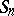 which are of cycle-type corresponding to partitions in
which are of cycle-type corresponding to partitions in 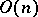 , with all parts odd, and in
, with all parts odd, and in 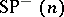 . The values of the spin characters can be given explicitly in the case
. The values of the spin characters can be given explicitly in the case 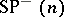 , but for
, but for 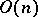 can be determined from a class of symmetric functions introduced for this purpose by Schur and now called Schur
can be determined from a class of symmetric functions introduced for this purpose by Schur and now called Schur 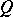 -functions (cf. Schur
-functions (cf. Schur 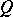 -function) — these play an analogous role to that of Schur functions for linear representations of
-function) — these play an analogous role to that of Schur functions for linear representations of  (cf. Schur functions in algebraic combinatorics). For each
(cf. Schur functions in algebraic combinatorics). For each 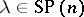 , let
, let 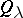 denote the corresponding Schur
denote the corresponding Schur 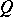 -function; then
-function; then
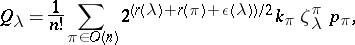 |
where 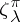 is the value of
is the value of 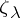 at the class of cycle-type
at the class of cycle-type 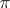 ,
, 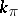 is the order of that class and
is the order of that class and 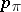 is the corresponding power-sum symmetric function and
is the corresponding power-sum symmetric function and 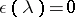 or
or 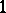 according as
according as 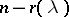 is even or odd. If
is even or odd. If 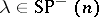 , then
, then
 |
and
 |
Schur also determined the dimension formula
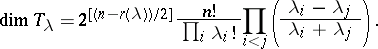 |
The spin representations of 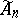 are now easily determined; if
are now easily determined; if 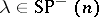 , then
, then 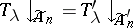 is an irreducible spin representation and if
is an irreducible spin representation and if  , then
, then 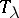 splits into two conjugate irreducible spin representations
splits into two conjugate irreducible spin representations 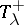 and
and 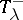 of equal dimension and
of equal dimension and
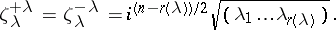 |
All these results appeared in Schur's 1911 paper [a11] — the subject then lay dormant until the appearance of papers by A.O. Morris in the early 1960{}s [a6], [a7], where the combinatorial concepts of bars and bar lengths were introduced (cf. Schur  -function); these correspond to the concepts of hooks and hook lengths in the linear case. Thus, the above dimension formula can be interpreted in terms of bar lengths:
-function); these correspond to the concepts of hooks and hook lengths in the linear case. Thus, the above dimension formula can be interpreted in terms of bar lengths:
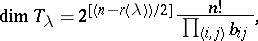 |
where 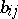 denotes the bar length at the
denotes the bar length at the 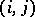 th node in the Young diagram corresponding to
th node in the Young diagram corresponding to 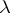 . Also, a recursion formula for calculating the irreducible spin characters analogous to the Murnaghan–Nakayama formula in the linear case was obtained in terms of these concepts. In all these formulas, as in the above dimension formula, the real difference is the complication added by the powers of
. Also, a recursion formula for calculating the irreducible spin characters analogous to the Murnaghan–Nakayama formula in the linear case was obtained in terms of these concepts. In all these formulas, as in the above dimension formula, the real difference is the complication added by the powers of  which appear.
which appear.
Totally lacking until the 1990 work of M.L. Nazarov [a8] were explicit methods for constructing the irreducible spin matrix representations corresponding to each partition 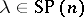 — these generalize the ones given by Schur for the partition
— these generalize the ones given by Schur for the partition 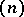 . The method is comparable to the classical construction of the semi-normal form given by A. Young (cf. Representation of the symmetric groups). More recently, Nazarov has generalized Young's symmetrizer to the spin case. However, there are presently (2000) no analogues developed to Specht modules (cf. Specht module).
. The method is comparable to the classical construction of the semi-normal form given by A. Young (cf. Representation of the symmetric groups). More recently, Nazarov has generalized Young's symmetrizer to the spin case. However, there are presently (2000) no analogues developed to Specht modules (cf. Specht module).
Some progress has been made on the modular spin representations of these groups. In 2001, the two papers [a2] and [a3] by J. Brundan and A. Kleshchev completely overturned the position. A conjecture corresponding to the classical Nakayama conjecture on the distribution of the spin characters into their 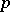 -blocks has been proved — but, in general, the position here is even less understood than in the case of the modular ordinary representations.
-blocks has been proved — but, in general, the position here is even less understood than in the case of the modular ordinary representations.
See [a1] for the most recent developments.
References
| [a1] | C. Bessenrodt, "Algebra and combinatorics" Progress in Math. , 168 (1998) pp. 64–91 |
| [a2] | J. Brundan, A. Kleshchev, "Projective representations of the symmetric group via Sergeev duality" Math. Z. (to appear) |
| [a3] | J. Brundan, A. Kleshchev, "Hecke–Clifford superalgebras, crystals of type 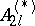 and modular branching rules for and modular branching rules for 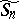 " (to appear) " (to appear) |
| [a4] | P.N. Hoffman, J.F. Humphreys, "Projective representations of the symmetric groups" , Oxford Univ. Press (1992) |
| [a5] | G. Karpilovsky, "Projective representations of finite groups" , M. Dekker (1995) |
| [a6] | A.O. Morris, "The spin representation of the symmetric group" Proc. London Math. Soc. , 12 : 3 (1962) pp. 55–76 |
| [a7] | A.O. Morris, "The spin representation of the symmetric group" Canad. J. Math. , 17 (1965) pp. 543–549 |
| [a8] | M.L. Nazarov, "Young's orthogonal form of irreducible projective representations of the symmetric group" J. London Math. Soc. , 42 : 2 (1990) pp. 437–451 |
| [a9] | I. Schur, "Über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 127 (1904) pp. 20–50 |
| [a10] | I. Schur, "Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 132 (1907) pp. 85–137 |
| [a11] | I. Schur, "Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 139 (1911) pp. 155–250 |
| [a12] | J.R. Stembridge, "Shifted tableaux and projective representations of symmetric groups" Adv. Math. , 74 (1989) pp. 87–134 |
Projective representations of symmetric and alternating groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_representations_of_symmetric_and_alternating_groups&oldid=14390