Projection methods
Methods for finding an approximate solution of an operator equation in a prescribed subspace, based on projecting the equation onto some (generally speaking, different) subspace. Projection methods constitute the basis for various computational schemes for solving boundary value problems, including the finite element and collocation methods (cf. Galerkin method; Collocation method).
Let 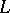 be an operator with domain of definition
be an operator with domain of definition 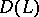 in a Banach space
in a Banach space 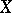 and with range
and with range 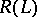 in a Banach space
in a Banach space 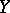 . To solve the equation
. To solve the equation
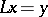 | (1) |
by a projection method, one chooses two sequences 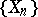 and
and 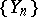 of subspaces
of subspaces
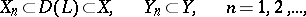 |
as well as projectors 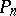 projecting
projecting  onto
onto 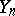 . Equation (1) is replaced by the approximate equation
. Equation (1) is replaced by the approximate equation
 | (2) |
In the case 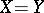 ,
, 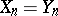 ,
,  the projection method (2) is usually called the Galerkin method (sometimes the latter method is interpreted in a wider sense, see Galerkin method).
the projection method (2) is usually called the Galerkin method (sometimes the latter method is interpreted in a wider sense, see Galerkin method).
A convergence theorem holds for projection methods for linear equations (in the case of finite-dimensional subspaces  and
and 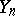 ). Suppose that
). Suppose that 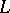 is linear and takes
is linear and takes 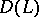 onto
onto 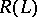 bijectively, with
bijectively, with 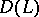 and
and 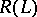 dense in
dense in 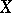 and
and 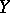 , respectively. Suppose that the subspaces
, respectively. Suppose that the subspaces 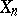 and
and 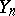 are finite-dimensional,
are finite-dimensional, 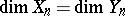 ,
,  and that the projectors
and that the projectors 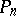 are uniformly bounded in
are uniformly bounded in  , that is,
, that is, 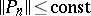 ,
, 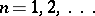 . Then the following condition a) is equivalent to the conditions b) and c) combined.
. Then the following condition a) is equivalent to the conditions b) and c) combined.
a) From some 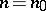 onwards there exists a unique solution
onwards there exists a unique solution 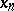 of (2), and
of (2), and 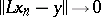 for any
for any 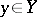 ;
;
b) The sequence of subspaces 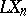 is dense in the limit in
is dense in the limit in 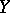 , that is, the distance
, that is, the distance  as
as  for every
for every 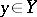 ;
;
c) 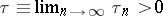 , where
, where  .
.
The rate of convergence under the conditions b) and c) is characterized by the inequality
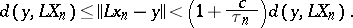 | (3) |
If 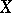 and
and  are Hilbert spaces and
are Hilbert spaces and 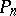 and
and  are orthoprojectors projecting
are orthoprojectors projecting 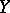 onto
onto 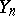 and
and 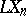 , respectively, condition c) is equivalent to the condition
, respectively, condition c) is equivalent to the condition
c') 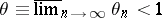 , where
, where 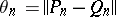 is the gap (angle) between the subspaces
is the gap (angle) between the subspaces 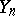 and
and 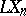 ; instead of (3) one obtains the estimate
; instead of (3) one obtains the estimate
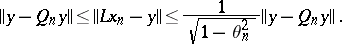 |
In case 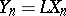 (the least-squares method) one has
(the least-squares method) one has 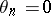 ,
,  and the convergence criterion is the condition b).
and the convergence criterion is the condition b).
The theorem yields a condition for convergence of the discrepancy 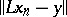 . If
. If 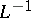 is bounded and
is bounded and 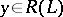 , then convergence of the discrepancy implies convergence of the approximations
, then convergence of the discrepancy implies convergence of the approximations 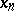 themselves to the solution
themselves to the solution 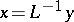 of equation (1). From the theorem, a convenient criterion for the convergence of the Galerkin method can be extracted; for the Galerkin–Petrov method an additional condition of the type c') should be imposed.
of equation (1). From the theorem, a convenient criterion for the convergence of the Galerkin method can be extracted; for the Galerkin–Petrov method an additional condition of the type c') should be imposed.
Suppose that 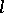 is a bounded linear form and
is a bounded linear form and  is a bounded bilinear form on a real Hilbert space
is a bounded bilinear form on a real Hilbert space  (or sesquilinear in the case of a complex
(or sesquilinear in the case of a complex 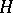 ). It is assumed that
). It is assumed that  is representable as
is representable as 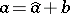 , such that
, such that
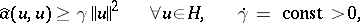 |
while the bilinear form 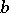 is completely continuous, i.e. the weak convergences
is completely continuous, i.e. the weak convergences 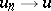 ,
,  in
in 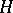 imply the convergence
imply the convergence 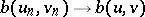 (the forms
(the forms 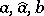 are not necessarily symmetric). Suppose that the following problem is posed: Find a
are not necessarily symmetric). Suppose that the following problem is posed: Find a  such that
such that
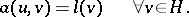 | (4) |
The Galerkin method for solving (4) consists in the following. One chooses (closed) subspaces 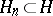 ,
, 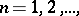 and finds a
and finds a  such that
such that
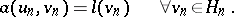 | (5) |
The following theorem holds: Suppose that  is dense in the limit in
is dense in the limit in 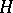 , that the conditions imposed above on
, that the conditions imposed above on  are satisfied and that problem (4) has a unique solution
are satisfied and that problem (4) has a unique solution 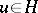 (an equivalent condition is: the homogeneous problem of finding
(an equivalent condition is: the homogeneous problem of finding  from the condition
from the condition  for every
for every 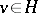 has only the trivial solution
has only the trivial solution 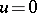 ); then problem (5) for sufficiently large
); then problem (5) for sufficiently large  has a unique solution
has a unique solution 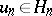 , and
, and  with the estimate
with the estimate
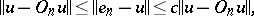 |
where 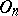 is the orthoprojector projecting
is the orthoprojector projecting 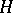 onto
onto 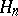 and
and 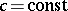 .
.
In applications to boundary value problems for equations of elliptic type, as a rule, the energy space of the principal part of the corresponding differential operator is chosen as 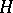 .
.
References
| [1] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
Comments
References
| [a1] | C.A.J. Fletcher, "Computational Galerkin methods" , Springer (1984) |
Projection methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projection_methods&oldid=15275