Profinite group
A topological group that is the projective limit of an inverse system of finite discrete groups 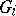 ,
, 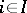 (where
(where  is a pre-ordered directed set). The profinite group
is a pre-ordered directed set). The profinite group 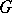 is denoted by
is denoted by 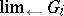 . As a subspace of the direct product
. As a subspace of the direct product 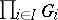 , endowed with the compact topology (a neighbourhood base of the identity is given by the system of kernels of the projections
, endowed with the compact topology (a neighbourhood base of the identity is given by the system of kernels of the projections 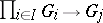 ), it is closed and hence compact.
), it is closed and hence compact.
Examples.
1) Let  be the set of integers larger than zero with the natural order relation, and let
be the set of integers larger than zero with the natural order relation, and let  . Suppose that
. Suppose that 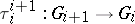 is the natural epimorphism, and put
is the natural epimorphism, and put
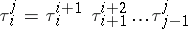 |
for all 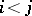 . Then
. Then 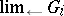 is the (additive) group of the ring
is the (additive) group of the ring 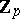 of
of 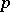 -adic integers.
-adic integers.
2) Every compact analytic group over a 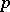 -adic number field (e.g.
-adic number field (e.g. 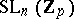 ) is profinite as a topological group.
) is profinite as a topological group.
3) Let 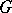 be an abstract group and let
be an abstract group and let 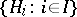 be the family of its normal subgroups of finite index. On
be the family of its normal subgroups of finite index. On 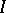 one introduces the relation
one introduces the relation 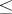 , putting
, putting  if
if 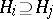 . This relation turns
. This relation turns  into a pre-ordered directed set. Associate to
into a pre-ordered directed set. Associate to 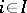 the group
the group  , and to each pair
, and to each pair 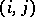 ,
, 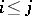 , the natural homomorphism
, the natural homomorphism 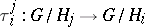 . One obtains the profinite group
. One obtains the profinite group 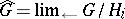 , called the profinite group completion of
, called the profinite group completion of 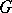 . It is the separable completion of
. It is the separable completion of 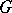 (cf. Separable completion of a ring) for the topology defined by the subgroups of finite index. The kernel of the natural homomorphism
(cf. Separable completion of a ring) for the topology defined by the subgroups of finite index. The kernel of the natural homomorphism 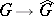 is the intersection of all subgroups of finite index. In this construction one can consider, instead of the family of all normal subgroups of finite index, only those whose index is a fixed power of a prime number
is the intersection of all subgroups of finite index. In this construction one can consider, instead of the family of all normal subgroups of finite index, only those whose index is a fixed power of a prime number 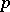 . The corresponding group is denoted by
. The corresponding group is denoted by 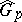 , and is a pro-
, and is a pro-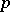 -group.
-group.
4) Profinite groups naturally arise in Galois theory of (not necessarily finite) algebraic extensions of fields in the following way. Let 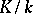 be a Galois extension and suppose that
be a Galois extension and suppose that 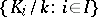 is the family of all finite Galois extensions of
is the family of all finite Galois extensions of 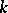 lying in
lying in 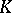 . Then
. Then  , and one can introduce on
, and one can introduce on 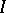 the relation
the relation 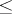 by putting
by putting 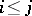 if
if 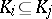 . The set
. The set 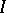 then becomes pre-ordered. Let
then becomes pre-ordered. Let 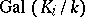 be the Galois group of
be the Galois group of 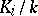 . To every pair
. To every pair 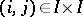 ,
, 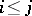 , one naturally associates the homomorphism
, one naturally associates the homomorphism
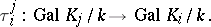 |
The corresponding profinite group 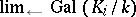 is isomorphic to
is isomorphic to 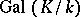 , thus
, thus 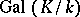 can be considered as a profinite group. The system
can be considered as a profinite group. The system 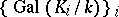 forms in
forms in  a neighbourhood base of the identity (cf. Galois topological group). This construction has a generalization in algebraic geometry in the definition of the fundamental group of a scheme.
a neighbourhood base of the identity (cf. Galois topological group). This construction has a generalization in algebraic geometry in the definition of the fundamental group of a scheme.
A profinite group can be characterized as a compact totally-disconnected group (cf. Compact group), as well as a compact group that has a system of open normal subgroups forming a neighbourhood base of the identity. The cohomology theory of profinite groups (cf. Cohomology of groups; Galois cohomology) plays an important role in modern Galois theory.
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [2] | H. Koch, "Galoissche Theorie der 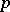 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Profinite group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Profinite_group&oldid=12021