Product of a family of objects in a category
A concept characterizing the notion of a Cartesian product in the language of morphisms. Let 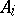 ,
, 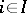 , be an indexed family of objects in the category
, be an indexed family of objects in the category 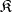 . An object
. An object 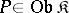 (together with morphisms
(together with morphisms 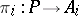 ,
, 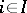 ) is called a product of the family of objects
) is called a product of the family of objects 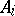 ,
, 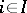 , if for every family of morphisms
, if for every family of morphisms 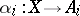 ,
, 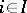 , there is a unique morphism
, there is a unique morphism 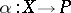 such that
such that 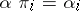 ,
, 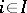 . The morphisms
. The morphisms 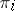 are called product projections; the product is denoted by
are called product projections; the product is denoted by 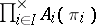 or
or 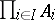 , or
, or 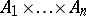 in the case
in the case 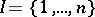 . The morphism
. The morphism 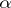 that occurs in the definition of the product is sometimes denoted by
that occurs in the definition of the product is sometimes denoted by 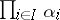 or
or 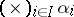 . The product of a family
. The product of a family 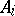 ,
, 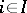 , is determined uniquely up to isomorphism; it is associative and commutative. The concept of the product of a family of objects is dual to that of a coproduct of a family of objects.
, is determined uniquely up to isomorphism; it is associative and commutative. The concept of the product of a family of objects is dual to that of a coproduct of a family of objects.
A product of the empty family of objects is a right zero (a terminal object) of the category. In most categories of structured sets (categories of sets, groups, topological spaces, etc.) the concept of the product of a family of objects coincides with the concept of the Cartesian (direct) product of these objects. Nevertheless, this coincidence is not necessary: In the category of torsion Abelian groups the product of a family of groups 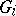 ,
, 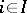 , is the torsion part of their Cartesian product, which in general is different from the Cartesian product itself.
, is the torsion part of their Cartesian product, which in general is different from the Cartesian product itself.
In categories with zero morphisms, for any product 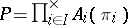 there exist uniquely defined morphisms
there exist uniquely defined morphisms 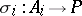 ,
, 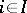 , such that
, such that 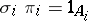 ,
, 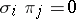 for
for 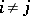 . If
. If 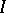 is finite and the category is additive, then
is finite and the category is additive, then 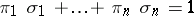 and the product of the family of objects
and the product of the family of objects 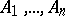 is also their coproduct.
is also their coproduct.
References
| [1] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
Comments
S. MacLane [a1] is generally credited with being the first to observe that Cartesian products could be described in purely categorical terms, as above.
References
| [a1] | S. MacLane, "Duality for groups" Bull. Amer. Math. Soc. , 56 (1950) pp. 485–516 |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
Product of a family of objects in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Product_of_a_family_of_objects_in_a_category&oldid=15014