Probability of large deviations
A probability of the type
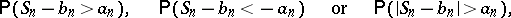 |
where
 |
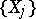 is a sequence of independent random variables, and
is a sequence of independent random variables, and 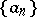 and
and 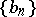 are two numerical sequences such that
are two numerical sequences such that 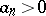 , and
, and 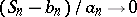 in probability.
in probability.
If the random variables 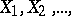 have the same distribution with mathematical expectation zero and finite variance
have the same distribution with mathematical expectation zero and finite variance 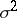 , one may write
, one may write 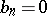 and
and  , where
, where 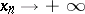 as
as 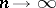 . Cramér's theorem and strengthened versions of it are particularly important in this connection (cf. Cramér theorem).
. Cramér's theorem and strengthened versions of it are particularly important in this connection (cf. Cramér theorem).
To obtain guaranteed bounds for the probability of large deviations one uses inequalities of the type of the Chebyshev inequality in probability theory; these provide the so-called exponential bounds for the probability of large deviations. For instance, if the random variables 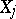 are independent,
are independent, 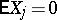 ,
, 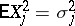 ,
, 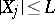 with probability one,
with probability one, 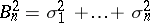 and
and 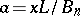 , then the estimate
, then the estimate
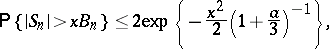 |
the right-hand side of which decreases exponentially with increasing  , is valid for all
, is valid for all 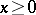 .
.
References
| [1] | M. Loève, "Probability theory" , Springer (1977) |
| [2] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [3] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) |
| [4] | Yu.V. Prokhorov, "Multidimensional distributions: inequalities and limit theorems" J. Soviet Math. , 2 : 5 (1976) pp. 475–488 Itogi Nauk. i Tekhn. , 10 (1972) pp. 5–24 |
| [5] | V.V. Yurinskii, "Exponential bounds for large deviations" Theory Probab. Appl. , 19 : 1 (1974) pp. 154–159 Teor. Veroyatnost. i Primenen. , 19 : 1 (1974) pp. 152–153 |
Comments
There are substantial new developments which link the rate of exponential decay to entropy. These developments find widespread use in statistical physics and in statistics. Cf. Limit theorems and [a1], [a2].
A second recent development concerns the development of limit theorems and large deviation theory for stochastic processes instead of sums of independent random variables, cf. [a3].
References
| [a1] | R.S. Ellis, "Entropy, large deviations, and statistical mechanics" , Springer (1985) |
| [a2] | D.W. Stroock, "An introduction to the theory of large deviations" , Springer (1984) |
| [a3] | A.D. [A.D. Ventsel'] Wentzell, "Limit theorems on large deviations for Markov stochastic processes" , Kluwer (1990) (Translated from Russian) |
| [a4] | H. Cramér, "Sur un nouveau théorème-limite de la théorie des probabilités" , Act. Sci. et Ind. , 736 , Hermann (1938) pp. 5–24 |
| [a5] | P. Groeneboom, J. Oosterhoff, F.H. Ruymgaart, "Large deviation theorems for empirical probability measures" Ann. Probl. , 7 (1979) pp. 553–586 |
Probability of large deviations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Probability_of_large_deviations&oldid=16113