Probabilistic metric space
Generalizations of metric spaces (cf. Metric space), in which the distances between points are specified by probability distributions (cf. Probability distribution) rather than numbers. The general notion was introduced by K. Menger in 1942 and has since been developed by a number of authors. A treatment, comprehensive up to 1983, may be found in [a1].
Let 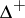 be the set of all functions
be the set of all functions 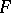 from the real line
from the real line 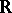 into the unit interval
into the unit interval 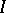 =
=
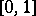 that are non-decreasing and left-continuous on
that are non-decreasing and left-continuous on  , and such that
, and such that 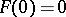 and
and 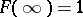 , i.e., the set of all probability distribution functions whose support lies in the extended half-line
, i.e., the set of all probability distribution functions whose support lies in the extended half-line 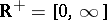 . For any
. For any 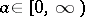 , let
, let 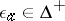 be defined by
be defined by 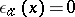 for
for 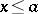 and
and 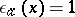 for
for 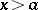 ; and let
; and let 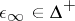 be defined by
be defined by 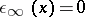 for all
for all 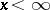 and
and 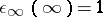 . Then, under the usual pointwise ordering of functions, given by
. Then, under the usual pointwise ordering of functions, given by 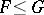 if and only if
if and only if 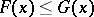 for all
for all 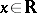 , the set
, the set 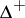 is a complete lattice with maximal element
is a complete lattice with maximal element 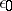 and minimal element
and minimal element 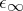 . There is a natural topological structure (topology) on
. There is a natural topological structure (topology) on 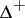 , namely, the topology of weak convergence (cf. also Weak topology), where
, namely, the topology of weak convergence (cf. also Weak topology), where 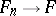 if and only if
if and only if 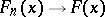 at every point of continuity of
at every point of continuity of 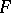 . Under this topology
. Under this topology 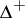 is compact and connected (cf. Compact space; Connected space); moreover, this topology can be metrized (cf. Metrizable space), e.g., by a variant of the Lévy metric.
is compact and connected (cf. Compact space; Connected space); moreover, this topology can be metrized (cf. Metrizable space), e.g., by a variant of the Lévy metric.
A triangle function is a binary operation  on
on 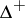 satisfying the following conditions:
satisfying the following conditions:
a) 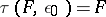 for all
for all 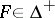 ;
;
b) 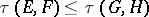 whenever
whenever 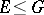 ,
, 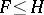 ;
;
c)  ;
;
d) 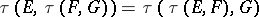 .
.
It is also often required that  be continuous with respect to the topology of weak convergence, or that
be continuous with respect to the topology of weak convergence, or that  satisfies the condition:
satisfies the condition:
e) 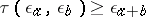 for all
for all 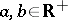 .
.
Examples of triangle functions are convolution and the functions 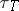 given by
given by
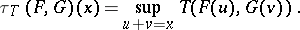 |
Here 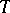 is a
is a 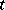 -norm, i.e., a binary operation on
-norm, i.e., a binary operation on 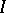 that, like
that, like  , has an identity element (the number
, has an identity element (the number 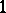 in this case) and is non-decreasing, commutative, and associative. Particular
in this case) and is non-decreasing, commutative, and associative. Particular 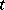 -norms are the functions
-norms are the functions 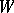 ,
,  , and
, and 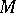 given, respectively, by
given, respectively, by 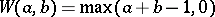 ,
, 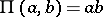 , and
, and  . The corresponding triangle functions
. The corresponding triangle functions 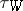 ,
, 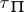 , and
, and 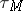 are continuous and satisfy e).
are continuous and satisfy e).
A probabilistic metric space is a triple 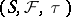 , where
, where  is a set,
is a set, 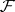 is a function from
is a function from 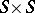 into
into 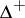 ,
,  is a triangle function, such that for any
is a triangle function, such that for any 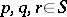 ,
,
I)  ;
;
II) 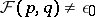 if
if 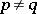 ;
;
III) 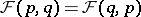 ;
;
IV) 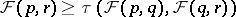 .
.
If  satisfies only I), III) and IV), then
satisfies only I), III) and IV), then  is a probabilistic pseudo-metric space.
is a probabilistic pseudo-metric space.
For any  and any
and any 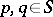 , the value of
, the value of 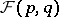 at
at  , usually denoted by
, usually denoted by 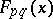 , is often interpreted as "the probability that the distance between p and q is less than x" .
, is often interpreted as "the probability that the distance between p and q is less than x" .
Thus, the generalization from ordinary to probabilistic metric spaces consists of:
1) replacing the range 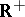 of the ordinary metric by the space of probability distributions
of the ordinary metric by the space of probability distributions 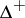 ;
;
2) replacing the operation of addition on  , which plays the pivotal role in the ordinary triangle inequality, by a triangle function. Note that for a function
, which plays the pivotal role in the ordinary triangle inequality, by a triangle function. Note that for a function  from
from 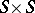 into
into  , if
, if  is defined via
is defined via 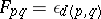 and if
and if  is a triangle function satisfying e), then
is a triangle function satisfying e), then  is an ordinary metric space; and conversely. If
is an ordinary metric space; and conversely. If 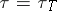 for some
for some  -norm
-norm  , then the probabilistic metric space is a Menger space.
, then the probabilistic metric space is a Menger space.
There is a natural topology on a probabilistic metric space, determined by the system of neighbourhoods 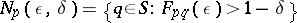 . However, a more interesting class of topological structures is obtained by designating a particular
. However, a more interesting class of topological structures is obtained by designating a particular  as a profile function, interpreting
as a profile function, interpreting  as the maximum confidence associated with distances less than
as the maximum confidence associated with distances less than  , and considering the system of neighbourhoods
, and considering the system of neighbourhoods
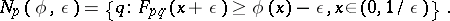 |
These determine a generalized topology (specifically, a closure space in the sense of E. Čech). There is also an associated indistinguishability relation, defined by  if and only if
if and only if 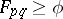 . This relation is a tolerance relation, i.e., is reflexive and symmetric, but not necessarily transitive.
. This relation is a tolerance relation, i.e., is reflexive and symmetric, but not necessarily transitive.
Let 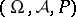 be a probability space,
be a probability space, 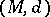 a metric space, and
a metric space, and 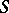 the set of all functions from
the set of all functions from  into
into 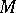 . For any
. For any 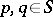 , define
, define 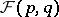 via
via
 |
Then IV) holds with 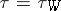 . The resultant probabilistic pseudo-metric space is called an
. The resultant probabilistic pseudo-metric space is called an 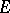 -space. For any
-space. For any 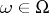 , the function
, the function 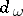 from
from 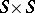 into
into 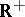 given by
given by 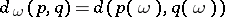 is a pseudo-metric on
is a pseudo-metric on 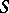 , and the
, and the 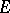 -space is pseudo-metrically generated in the sense that
-space is pseudo-metrically generated in the sense that
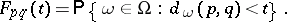 |
Conversely, any such pseudo-metrically generated space is an 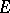 -space. An important class of
-space. An important class of 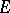 -spaces is obtained when
-spaces is obtained when  is the Euclidean
is the Euclidean  -dimensional space and
-dimensional space and 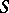 is the set of all non-degenerate
is the set of all non-degenerate  -dimensional spherically symmetric Gaussian vectors.
-dimensional spherically symmetric Gaussian vectors.
The idea behind the construction of an 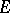 -space has been generalized. For example, if
-space has been generalized. For example, if 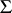 is a set with some structure, e.g., a normed, inner product or topological space, then the set of all functions from
is a set with some structure, e.g., a normed, inner product or topological space, then the set of all functions from 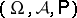 into
into 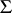 yields a space in which that structure is probabilistic. This idea has recently been applied in cluster analysis, where the numerical dissimilarity coefficient has been replaced by an element of
yields a space in which that structure is probabilistic. This idea has recently been applied in cluster analysis, where the numerical dissimilarity coefficient has been replaced by an element of 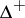 . The result is a theory of percentile clustering [a2]. The principal advantage of percentile clustering methods is that, when working with distributed data, they permit one to classify first and then summarize, instead of summarizing first and then classifying.
. The result is a theory of percentile clustering [a2]. The principal advantage of percentile clustering methods is that, when working with distributed data, they permit one to classify first and then summarize, instead of summarizing first and then classifying.
Let 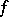 be a function from a metric space
be a function from a metric space  into itself, and, for any non-negative integer
into itself, and, for any non-negative integer 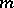 , let
, let  denote the
denote the  th iterate of
th iterate of 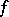 . For any
. For any 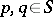 , define the sequence
, define the sequence 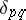 by
by
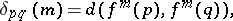 |
and for any positive integer  define
define 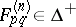 via
via
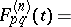 |
 |
where 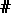 denotes the cardinality of the set in question. The number
denotes the cardinality of the set in question. The number 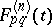 may be interpreted as the probability that the distance between the initial segments, of length
may be interpreted as the probability that the distance between the initial segments, of length  , of the trajectories of
, of the trajectories of 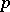 and
and 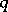 is less than
is less than 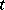 . Let
. Let
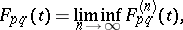 |
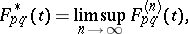 |
and let 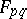 and
and 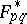 be normalized to be left-continuous, hence in
be normalized to be left-continuous, hence in  . If
. If  is defined via
is defined via 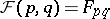 , then, again, IV) holds with
, then, again, IV) holds with 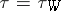 . The resultant probabilistic pseudo-metric space is a transformation generated space. Note that
. The resultant probabilistic pseudo-metric space is a transformation generated space. Note that 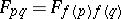 , so that
, so that 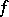 is (probabilistic) distance-preserving.
is (probabilistic) distance-preserving.
If 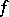 is measure-preserving (cf. Measure-preserving transformation) with respect to a probability measure
is measure-preserving (cf. Measure-preserving transformation) with respect to a probability measure 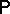 on
on  , then
, then 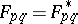 for almost all pairs
for almost all pairs 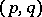 in
in  ; and if, in addition,
; and if, in addition, 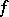 is mixing, then there is a
is mixing, then there is a 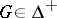 such that
such that  for almost all pairs
for almost all pairs 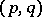 .
.
The above ideas play an important role in chaos theory. For example, if  is a closed interval
is a closed interval 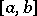 , if
, if 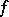 is continuous, and if there is a single pair of points
is continuous, and if there is a single pair of points  for which
for which 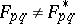 , then
, then 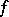 is chaotic in a very strong sense. This fact leads to a theory of distributional chaos. Specifically, if
is chaotic in a very strong sense. This fact leads to a theory of distributional chaos. Specifically, if 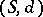 is compact, then
is compact, then  is distributionally chaotic if and only if there is a pair of points
is distributionally chaotic if and only if there is a pair of points 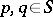 for which
for which 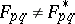 . Furthermore, the number
. Furthermore, the number
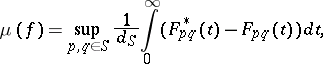 |
where 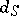 is the diameter of
is the diameter of 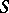 , provides a useful measure of the degree of distributional chaos. For details see [a3], [a4].
, provides a useful measure of the degree of distributional chaos. For details see [a3], [a4].
References
| [a1] | B. Schweizer, A. Sklar, "Probabilistic metric spaces" , Elsevier & North-Holland (1983) |
| [a2] | M.F. Janowitz, B. Schweizer, "Ordinal and percentile clustering" Math. Social Sci. , 18 (1989) pp. 135–186 |
| [a3] | B. Schweizer, J. Smítal, "Measures of chaos and a spectral decomposition of dynamical systems on the interval" Trans. Amer. Math. Soc. , 344 (1994) pp. 737–754 |
| [a4] | B. Schweizer, A. Sklar, J. Smítal, "Distributional (and other) chaos and its measurement" (to appear) |
Probabilistic metric space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Probabilistic_metric_space&oldid=15491