Principle of least reaction
From Encyclopedia of Mathematics
A corollary of Gauss' principle (cf. Gauss principle), obtained from the latter by using the equations representing Newton's second law for points of a constrained system (see [1]). According to the principle of least reaction, for the real motion of a system the quantity
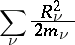 |
is minimal with respect to all motions conceivable in Gauss' sense. Here 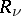 are the reactions of the constraints and
are the reactions of the constraints and 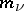 the masses of the points in the system.
the masses of the points in the system.
References
| [1] | N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian) |
Comments
References
| [a1] | R.B. Lindsay, H. Margenau, "Foundations of physics" , Dover, reprint (1957) |
How to Cite This Entry:
Principle of least reaction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principle_of_least_reaction&oldid=11914
Principle of least reaction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principle_of_least_reaction&oldid=11914
This article was adapted from an original article by V.V. Rumyantsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article