Principal series
of length 
A finite descending chain
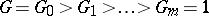 |
of normal subgroups of a group 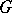 that cannot be included (without repetition) in any other chain with the same properties, i.e.
that cannot be included (without repetition) in any other chain with the same properties, i.e.  is a maximal normal subgroup of
is a maximal normal subgroup of  contained in
contained in  as a proper subgroup,
as a proper subgroup,  . A group has at least one principal series if and only if all ascending and descending chains of normal subgroups have finite length. If a group has two principal series, then they are isomorphic, i.e. they have the same length and there exists a bijection between the set of quotients
. A group has at least one principal series if and only if all ascending and descending chains of normal subgroups have finite length. If a group has two principal series, then they are isomorphic, i.e. they have the same length and there exists a bijection between the set of quotients  of one series and the set of quotients of the other series, corresponding factors being isomorphic.
of one series and the set of quotients of the other series, corresponding factors being isomorphic.
Comments
The terminology "principal series" is almost never used in the West. Instead one uses chief series. The isomorphism statement above is the Jordan–Hölder theorem for chief series. The quotients  defined by a chief series are called chief factors. Any chief series can be refined to a composition series (cf. Composition sequence).
defined by a chief series are called chief factors. Any chief series can be refined to a composition series (cf. Composition sequence).
References
| [a1] | R. Carmichael, "Groups of finite order" , Dover, reprint (1956) pp. 97 |
| [a2] | M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 124 |
| [a3] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) pp. 64 |
Principal series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_series&oldid=13785