Principal part of a differential operator
The homogeneous differential operator formed from the given operator by discarding all the terms not containing derivatives of maximal order. The principal part of the differential operator
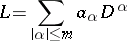 |
is 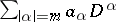 . The principal part of a differential operator is sometimes defined by the introduction of supplementary weights assigned to the differentiations with respect to the various arguments. For instance, the principal part of the differential operator
. The principal part of a differential operator is sometimes defined by the introduction of supplementary weights assigned to the differentiations with respect to the various arguments. For instance, the principal part of the differential operator 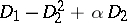 is sometimes defined as
is sometimes defined as 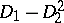 (if
(if 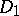 is given weight 2 and
is given weight 2 and  weight 1).
weight 1).
Comments
The principal part is also called the principal symbol (cf. also Symbol of an operator).
The zero sets of the principal symbol are called the characteristics of 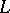 (cf. also Characteristic).
(cf. also Characteristic).
Further, a constant-coefficient differential operator 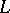 in
in 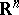 is said to be of real principal type if the principal symbol
is said to be of real principal type if the principal symbol 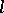 is real and if
is real and if  for
for 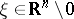 (cf. also Principal type, partial differential operator of).
(cf. also Principal type, partial differential operator of).
For a differential operator 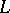 of order
of order 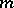 with
with 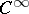 coefficients in a
coefficients in a 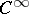 -manifold
-manifold 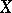 the principal symbol can be regarded as an invariantly-defined function on the cotangent bundle of
the principal symbol can be regarded as an invariantly-defined function on the cotangent bundle of 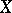 .
.
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) |
Principal part of a differential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_part_of_a_differential_operator&oldid=18800