Principal ideal
An ideal (of a ring, algebra, semi-group, or lattice) generated by one element  , i.e. the smallest ideal containing the element
, i.e. the smallest ideal containing the element  .
.
The left principal ideal  of a ring
of a ring  contains, in addition to the element
contains, in addition to the element  itself, also all the elements
itself, also all the elements
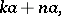 |
the right principal ideal  contains all the elements
contains all the elements
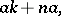 |
and the two-sided principal ideal  contains all elements of the form
contains all elements of the form
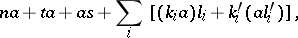 |
where  are arbitrary elements of
are arbitrary elements of  and
and 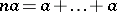 (
( terms,
terms,  ). If
). If  is a ring with a unit element, the term
is a ring with a unit element, the term 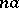 may be omitted. In particular, for an algebra
may be omitted. In particular, for an algebra  over a field,
over a field,
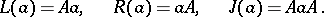 |
In a semi-group 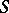 one also has left, right and two-sided ideals generated by an element
one also has left, right and two-sided ideals generated by an element  , and they are equal, respectively, to
, and they are equal, respectively, to
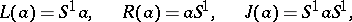 |
where 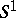 is the semi-group coinciding with
is the semi-group coinciding with  if
if 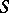 contains a unit, and is otherwise obtained from
contains a unit, and is otherwise obtained from  by external adjunction of a unit.
by external adjunction of a unit.
The principal ideal of a lattice 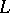 generated by an element
generated by an element  is identical with the set of all
is identical with the set of all  such that
such that 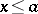 ; it is usually denoted by
; it is usually denoted by 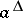 ,
, 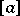 , or
, or  if the lattice has a zero. Thus,
if the lattice has a zero. Thus,
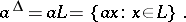 |
In a lattice of finite length all ideals are principal.
Comments
Let  be an integral domain with field of fractions
be an integral domain with field of fractions  . A principal fractional ideal of
. A principal fractional ideal of 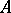 is an
is an  -submodule of
-submodule of  of the form
of the form  for some
for some 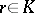 .
.
Let  be a lattice. Dual to the principal ideal generated by
be a lattice. Dual to the principal ideal generated by  one has the principal dual ideal or principal filter determined by
one has the principal dual ideal or principal filter determined by  , which is the set
, which is the set 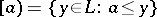 . The principal ideal in
. The principal ideal in  determined by
determined by  is also denoted (more accurately) by
is also denoted (more accurately) by  .
.
A partially ordered set is a complete lattice if and only if it has a zero and every ideal in  is principal.
is principal.
References
| [a1] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1963) pp. Chapt. IV, Sect. 3 (Translated from Russian) |
| [a2] | L. Beran, "Orthomodular lattices" , Reidel (1985) pp. 4ff |
| [a3] | G. Grätzer, "Lattice theory" , Freeman (1971) |
| [a4] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) pp. 78; 86; 162 (Translated from Russian) |
Principal ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_ideal&oldid=12133