Primitive recursion
A means of defining functions with natural number arguments and values. One says that an 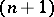 -place function
-place function 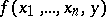 is obtained by primitive recursion from an
is obtained by primitive recursion from an  -place function
-place function 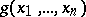 and an
and an 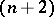 -place function
-place function 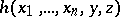 if for all natural number values of
if for all natural number values of 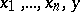 one has
one has
 |
and
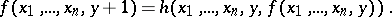 |
For given 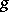 and
and 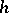 such a function
such a function 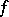 exists always and is unique. For
exists always and is unique. For 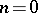 the defining equations for
the defining equations for 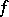 can be written as
can be written as
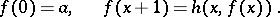 |
A fundamental property of primitive recursion is that for any meaningful specification of the notion of computability, a function 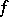 obtained from computable functions
obtained from computable functions 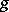 and
and 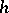 by means of primitive recursion is itself computable (cf. Computable function). Primitive recursion is one of the basic ways for generating all primitive recursive and all partial recursive functions from an initial set of basic functions (cf. Primitive recursive function; Partial recursive function).
by means of primitive recursion is itself computable (cf. Computable function). Primitive recursion is one of the basic ways for generating all primitive recursive and all partial recursive functions from an initial set of basic functions (cf. Primitive recursive function; Partial recursive function).
References
| [1] | V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian) |
| [2] | A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [3] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
Comments
References
| [a1] | C. Calude, "Theories of computational complexity" , North-Holland (1988) |
| [a2] | Yu.I. Manin, "A course in mathematical logic" , Springer (1977) (Translated from Russian) |
| [a3] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1959) pp. Chapts. IX; XI, §54 |
| [a4] | P. Odifreddi, "Classical recursion theory" , North-Holland (1989) pp. Chapt. II; esp. pp. 199ff |
Primitive recursion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_recursion&oldid=17879