Primitive function
anti-derivative, of a finite function 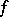
A function 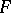 such that
such that 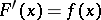 everywhere in the domain of definition of
everywhere in the domain of definition of 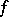 . This definition is the one most widely used, but others occur, in which the requirements on the existence of a finite
. This definition is the one most widely used, but others occur, in which the requirements on the existence of a finite 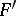 everywhere are weakened, as are those on the equation
everywhere are weakened, as are those on the equation 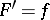 everywhere; a generalized derivative is sometimes used in the definition. Most of the theorems on primitive functions concern their existence, determination and uniqueness. A sufficient condition for the existence of a primitive function of a function
everywhere; a generalized derivative is sometimes used in the definition. Most of the theorems on primitive functions concern their existence, determination and uniqueness. A sufficient condition for the existence of a primitive function of a function  given on an interval is that
given on an interval is that 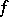 is continuous; necessary conditions are that
is continuous; necessary conditions are that 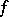 should belong to the first Baire class (cf. Baire classes) and that it has the Darboux property. Any two primitive functions of a function given on an interval differ by a constant. The task of finding
should belong to the first Baire class (cf. Baire classes) and that it has the Darboux property. Any two primitive functions of a function given on an interval differ by a constant. The task of finding 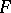 from
from 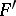 for continuous
for continuous 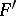 is solved by the Riemann integral, for bounded
is solved by the Riemann integral, for bounded 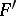 — by the Lebesgue integral, and for any
— by the Lebesgue integral, and for any 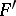 — by the Denjoy integral in the narrow (or wide) sense and the Perron integral.
— by the Denjoy integral in the narrow (or wide) sense and the Perron integral.
References
| [1] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1 , Moscow (1981) (In Russian) |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
The Darboux property or intermediate-value property of a real-valued function 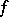 on an interval
on an interval 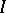 says that if
says that if 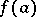 and
and 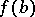 are two values of
are two values of 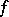 ,
, 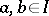 , then
, then 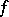 assumes any value between
assumes any value between 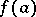 and
and 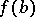 at some point between
at some point between  and
and 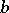 . Continuous functions have the intermediate-value property (the intermediate-value theorem). The fact that the derivative of a one-time differentiable real-valued function on an interval has the intermediate-value property is sometimes referred to as Darboux's theorem. It is an immediate consequence of the Rolle theorem.
. Continuous functions have the intermediate-value property (the intermediate-value theorem). The fact that the derivative of a one-time differentiable real-valued function on an interval has the intermediate-value property is sometimes referred to as Darboux's theorem. It is an immediate consequence of the Rolle theorem.
See also (the editorial comments to) Derivative.
References
| [a1] | R.P Boas jr., "A primer of real functions" , Math. Assoc. Amer. (1981) |
| [a2] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
Primitive function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_function&oldid=33749