Prime element
A generalization of the notion of a prime number. Let  be an integral domain or commutative semi-group with an identity. A non-zero element
be an integral domain or commutative semi-group with an identity. A non-zero element  that is not a divisor of unity is called prime if a product
that is not a divisor of unity is called prime if a product  can be divided by
can be divided by  only if one of the elements
only if one of the elements  or
or  can be divided by
can be divided by  . Every prime element is irreducible, i.e. is divisible only by divisors of unity or elements associated to it. An irreducible element need not be prime; however, in a Gauss semi-group both concepts coincide. Moreover, if every irreducible element of a semi-group
. Every prime element is irreducible, i.e. is divisible only by divisors of unity or elements associated to it. An irreducible element need not be prime; however, in a Gauss semi-group both concepts coincide. Moreover, if every irreducible element of a semi-group  is prime, then
is prime, then  is a Gauss semi-group. Analogous statements hold for a factorial ring. An element of a ring is prime if and only if the principal ideal generated by this element is a prime ideal.
is a Gauss semi-group. Analogous statements hold for a factorial ring. An element of a ring is prime if and only if the principal ideal generated by this element is a prime ideal.
There are generalizations of these notions to the non-commutative case (cf. [2]).
References
| [1] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1971) |
| [2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1974) |
Comments
Two elements 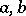 in a commutative semi-group or in an integral domain are associates of each other if each is a divisor of the other; i.e., if there are
in a commutative semi-group or in an integral domain are associates of each other if each is a divisor of the other; i.e., if there are 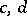 such that
such that 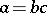 ,
,  .
.
Prime element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prime_element&oldid=12221