Primary ring
From Encyclopedia of Mathematics
A ring with a unit whose quotient ring with respect to the Jacobson radical is isomorphic to a matrix ring over a skew field, or, which is the same, is an Artinian simple ring. If the idempotents of a primary ring 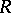 with Jacobson radical
with Jacobson radical 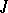 can be lifted modulo
can be lifted modulo 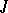 (i.e. for every idempotent of
(i.e. for every idempotent of 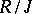 there is an idempotent pre-image in
there is an idempotent pre-image in 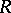 ), then
), then 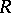 is isomorphic to the full matrix ring of a local ring. This holds, in particular, if
is isomorphic to the full matrix ring of a local ring. This holds, in particular, if 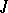 is a nil ideal.
is a nil ideal.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [2] | C. Faith, "Algebra" , 1–2 , Springer (1973–1976) |
Comments
See also Nil ideal.
How to Cite This Entry:
Primary ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primary_ring&oldid=17882
Primary ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primary_ring&oldid=17882
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article