Predator-prey system
A system of two species, one feeding on the other (cf. [a1], [a2], [a3], [a4], [a5], [a6]). A variety of mathematical approaches is used when modelling a predator-prey system, since there are many factors that can influence its evolution, e.g. predation-mediated coexistence, the size of habitat, hierarchical ranking, voracity and fertility of species, competition, inhomogeneity with respect to the age structure, latent, infection and incubation lags, seasonal changes, space diffusion, pollution, spatial environment heterogeneity, finite acceptance time for external signals, carrying capacity, permanence (persistence), etc. Isolating those factors which have to be taken into consideration and neglecting the others, one obtains different mathematical predator-prey models, described by different types of equations: ordinary, partial or functional differential equations, deterministic or stochastic, discrete or continuous etc.
Lotka–Volterra model.
This model, which takes into account only intrinsic phenomena (voracity and fertility), has the form
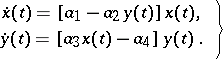 | (a1) |
Here,  is the number of preys,
is the number of preys, 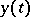 is the number of predators, and the
is the number of predators, and the 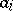 are positive constants (
are positive constants (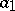 is the rate of birth of preys,
is the rate of birth of preys, 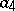 is the rate of death of predators,
is the rate of death of predators, 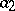 is a measure of susceptibility of preys to predation, and
is a measure of susceptibility of preys to predation, and  is the predatory ability). The system (a1) has a unique non-zero equilibrium position, which is a stable centre. At the same time, the solutions of (a1) are not structurally stable with respect to disturbance of initial conditions (cf. Rough system).
is the predatory ability). The system (a1) has a unique non-zero equilibrium position, which is a stable centre. At the same time, the solutions of (a1) are not structurally stable with respect to disturbance of initial conditions (cf. Rough system).
Models with intraspecific strife.
Within the restrictive domain of quadratic differential equations, those which include competition as well as predation should be somewhat more realistic. An example of a model with competition inside preys is given by:
 | (a2) |
where 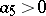 characterizes competition inside preys. Under biologically reasonable assumptions,
characterizes competition inside preys. Under biologically reasonable assumptions,  , and (a2) has a unique positive equilibrium which is an asymptotically-stable focus or node (cf. Focus; Node; Asymptotically-stable solution).
, and (a2) has a unique positive equilibrium which is an asymptotically-stable focus or node (cf. Focus; Node; Asymptotically-stable solution).
Kolmogorov predator-prey model.
This model can be written in the form
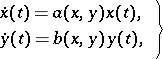 | (a3) |
under appropriate conditions on the functions 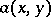 ,
, 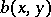 and their derivatives, reflecting a number of real phenomena, such as satiation. Node, focus and limit cycles (cf. Limit cycle) are among the possible behaviours of (a3).
and their derivatives, reflecting a number of real phenomena, such as satiation. Node, focus and limit cycles (cf. Limit cycle) are among the possible behaviours of (a3).
Delay effects.
To achieve some degree of realism, delay effects have to be taken into account. Moreover, many phenomena, like instability, oscillation and periodic change, cannot be explained without implementing delays into the model. To account for delay of feeding on reproduction, V. Volterra introduced the equations
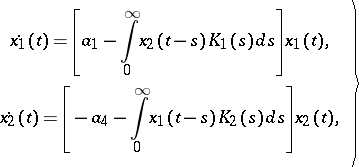 | (a4) |
where 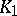 and
and 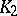 are finite positive continuous functions. The system (a4) leads to a stable aperiodic oscillation. Other types of integro-differential [a7] and, more general, functional-differential equations [a8], [a9], [a10] are widely used to develop predator-prey models of moderate mathematical complexity while not sacrificing biological realism.
are finite positive continuous functions. The system (a4) leads to a stable aperiodic oscillation. Other types of integro-differential [a7] and, more general, functional-differential equations [a8], [a9], [a10] are widely used to develop predator-prey models of moderate mathematical complexity while not sacrificing biological realism.
Discrete-time models.
The discrete version of (a3) is:
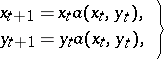 | (a5) |
where the functions  and
and 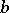 relate the predator-influenced reproductive efficiency of the prey and the searching of the predator, respectively. Even a simple version of (a5) can exhibit rich dynamics, from stability to chaos. For example, the equation (with
relate the predator-influenced reproductive efficiency of the prey and the searching of the predator, respectively. Even a simple version of (a5) can exhibit rich dynamics, from stability to chaos. For example, the equation (with  a constant parameter)
a constant parameter)
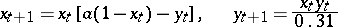 |
has an asymptotically-stable fixed point for 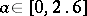 , an invariant circle for
, an invariant circle for 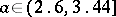 , and an attracting set for
, and an attracting set for 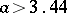 .
.
Predator-prey system with spatial inhomogeneity.
Such a system can be modelled by partial differential equations. Let 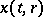 ,
, 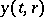 denote the prey and predator densities at time
denote the prey and predator densities at time 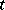 at the space point
at the space point  . Then, under the assumption that all dispersal occurs solely by simple diffusion processes, the predator-prey model has the form of reaction-diffusion equations (cf. Reaction-diffusion equation):
. Then, under the assumption that all dispersal occurs solely by simple diffusion processes, the predator-prey model has the form of reaction-diffusion equations (cf. Reaction-diffusion equation):
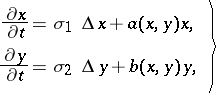 | (a6) |
where  are the diffusion rates and
are the diffusion rates and 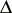 is the Laplace operator. If the diffusion rates
is the Laplace operator. If the diffusion rates 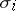 are increasing, then
are increasing, then  ,
,  become spatially homogeneous for large
become spatially homogeneous for large 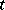 , i.e. the behaviour of this predator-prey system can be described by (a3). Diffusion in (a6) can generate instability, just opposite to its usual interpretation as a smoothing mechanism. In order to incorporate different realistic effects, it is often necessary to introduce time delays into the governing equations (a6) as well.
, i.e. the behaviour of this predator-prey system can be described by (a3). Diffusion in (a6) can generate instability, just opposite to its usual interpretation as a smoothing mechanism. In order to incorporate different realistic effects, it is often necessary to introduce time delays into the governing equations (a6) as well.
Predator-prey models with uncertainties of various origins.
These can be described by stochastic equations, e.g. of the form (a3), (a5) or (a6), where  and
and 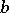 are stochastic processes (cf. also Stochastic differential equation).
are stochastic processes (cf. also Stochastic differential equation).
References
| [a1] | V. Volterra, "Théorie mathématique de la lutte pour la vie" , Gauthier-Villars (1931) |
| [a2] | A.J. Lotka, "Elements of physical biology" , Williams and Witkins (1925) |
| [a3] | A.N. Kolmogoroff, "Sulla theoria di Volterra della lotta per l'esistenza" Giorn. Inst. Ital. Attuari , 7 (1936) pp. 74–80 |
| [a4] | V.A. Kostitzin, "Mathematical biology" , Harrap (1939) |
| [a5] | M. Smith, "Models in ecology" , Cambridge Univ. Press (1974) |
| [a6] | J. Murray, "Mathematical biology" , Springer (1989) |
| [a7] | C.M. Cushing, "Integro-differential equations and delay models in population dynamics" , Lecture Notes in Biomathematics , 20 , Springer (1977) |
| [a8] | V.B. Kolmanovskii, A.D. Myshkis, "Applied theory of functional differential equations" , Kluwer Acad. Publ. (1992) (In Russian) |
| [a9] | Y. Kuang, "Delay differential equations with applications in population dynamics" , Acad. Press (1993) |
| [a10] | K. Gopalsamy, "Equations of mathematical ecology" , Kluwer Acad. Publ. (1992) |
Predator-prey system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predator-prey_system&oldid=15777