Pre-sheaf
From Encyclopedia of Mathematics
on a topological space 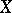 with values in a category
with values in a category  (e.g. the category of sets, groups, modules, rings, etc.)
(e.g. the category of sets, groups, modules, rings, etc.)
A contravariant functor 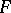 from the category of open sets of
from the category of open sets of 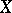 and their natural inclusion mappings into
and their natural inclusion mappings into 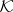 . Depending on
. Depending on  , the functor
, the functor 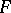 is called a pre-sheaf of sets, groups, modules, rings, etc. The morphisms
is called a pre-sheaf of sets, groups, modules, rings, etc. The morphisms 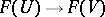 corresponding to the inclusions
corresponding to the inclusions 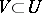 are called restriction homomorphisms.
are called restriction homomorphisms.
Every pre-sheaf generates a sheaf on  (cf. Sheaf theory).
(cf. Sheaf theory).
Comments
More generally, if  is any small category, the term "pre-sheaf on C" is used to denote a contravariant (usually set-valued) functor defined on
is any small category, the term "pre-sheaf on C" is used to denote a contravariant (usually set-valued) functor defined on 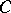 (cf. Site).
(cf. Site).
How to Cite This Entry:
Pre-sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-sheaf&oldid=16592
Pre-sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-sheaf&oldid=16592
This article was adapted from an original article by E.G. Sklyarenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article