Power of a statistical test
From Encyclopedia of Mathematics
The probability with which a statistical test for testing a simple hypothesis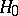 
against a simple hypothesis 
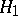rejects 
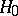when in fact 
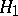is true. In the case when the hypothesis 
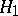, competing with 
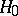in the test, is compound (
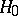itself may be either simple or compound, which is written symbolically: 
: 
, 
: 
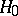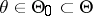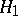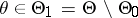), the power of the statistical test for 
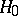against 
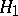is defined as the restriction of the power function 
, 
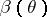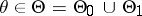, of this test to 
.
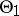In addition, this definition has been broadly generalized to the following: The power of a statistical test for testing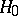 
: 
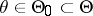against a compound alternative 
: 
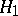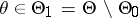is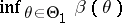 
, where 
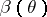is the power function of the test (see Power function of a test).
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959) |
| [2] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [3] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [4] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
How to Cite This Entry:
Power of a statistical test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_of_a_statistical_test&oldid=18477
Power of a statistical test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_of_a_statistical_test&oldid=18477
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article